Exam 17: Markov Processes

Two airlines offer conveniently scheduled flights to the airport nearest your corporate headquarters.Historically,flights have been scheduled as reflected in this transition matrix. 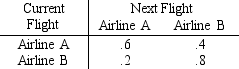a.If your last flight was on B,what is the probability your next flight will be on A? b.If your last flight was on B,what is the probability your second next flight will be on A? c.What are the steady state probabilities?

Steady state probabilities are independent of initial state.

Transition probabilities are conditional probabilities.

Appointments in a medical office are scheduled every 15 minutes.Throughout the day,appointments will be running on time or late,depending on the previous appointment only,according to the following matrix of transition probabilities: 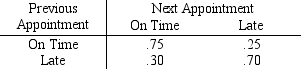a.The day begins with the first appointment on time.What are the state probabilities for periods 1,2,3 and 4? b.What are the steady state probabilities?

A unique matrix of transition probabilities should be developed for each customer.

Analysis of a Markov process

In Markov analysis,we are concerned with the probability that the

If the probability of making a transition from a state is 0,then that state is called a(n)

A television ratings company surveys 100 viewers on March 1 and April 1 to find what was being watched at 6:00 p.m.-- the local NBC affiliate's local news,the CBS affiliate's local news,or "Other" which includes all other channels and not watching TV.The results show 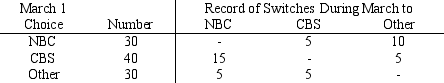a.What are the numbers in each choice for April 1? b.What is the transition matrix? c.What ratings percentages do you predict for May 1?

Rent-To-Keep rents household furnishings by the month.At the end of a rental month a customer can: a)rent the item for another month,b)buy the item,or c)return the item.The matrix below describes the month-to-month transition probabilities for 32-inch stereo televisions the shop stocks. What is the probability that a customer who rented a TV this month will eventually buy it?

Accounts receivable have been grouped into the following states: State 1: Paid State 2: Bad debt State 3: 0?30 days old State 4: 31?60 days old Sixty percent of all new bills are paid before they are 30 days old.The remainder of these go to state 4.Seventy percent of all 30 day old bills are paid before they become 60 days old.If not paid,they are permanently classified as bad debts. a.Set up the one month Markov transition matrix. b.What is the probability that an account in state 3 will be paid?

When absorbing states are present,each row of the transition matrix corresponding to an absorbing state will have a single 1 and all other probabilities will be 0.

The fundamental matrix is used to calculate the probability of the process moving into each absorbing state.

All entries in a row of a matrix of transition probabilities sum to 1.

At steady state

A state i is an absorbing state if p_ii = 0.

The daily price of a farm commodity is up,down,or unchanged from the day before.Analysts predict that if the last price was down,there is a .5 probability the next will be down,and a .4 probability the price will be unchanged.If the last price was unchanged,there is a .35 probability it will be down and a .35 probability it will be up.For prices whose last movement was up,the probabilities of down,unchanged,and up are .1,.3,and .6. a.Construct the matrix of transition probabilities. b.Calculate the steady state probabilities.

All entries in a matrix of transition probabilities sum to 1.

For Markov processes having the memoryless property,the prior states of the system must be considered in order to predict the future behavior of the system.

The probability of reaching an absorbing state is given by the