Explore all topics
Start Free Trial
Need Help? Contact us
back arrowfull exam logo
search
ai logoChat with AI
Servicesarrow
Discoverarrow

Topics

Explore all topics
Discover more topics

Exam 13: Project Scheduling: Pertcpm

arrow
Exam 1: Introduction50 Questionsadd course
Exam 2: Introduction to Probability53 Questionsadd course
Exam 3: Probability Distributions52 Questionsadd course
Exam 4: Decision Analysis48 Questionsadd course
Exam 5: Utility and Game Theory49 Questionsadd course
Exam 6: Forecasting60 Questionsadd course
Exam 7: Introduction to Linear Programming54 Questionsadd course
Exam 8: Lp Sensitivity Analysis and Interpretation of Solution49 Questionsadd course
Exam 9: Linear Programming Applications42 Questionsadd course
Exam 10: Distribution and Network Problems57 Questionsadd course
Exam 11: Integer Linear Programming49 Questionsadd course
Exam 12: Advanced Optimization Application42 Questionsadd course
Exam 13: Project Scheduling: Pertcpm41 Questionsadd course
Exam 14: Inventory Models54 Questionsadd course
Exam 15: Waiting Line Models52 Questionsadd course
Exam 16: Simulation49 Questionsadd course
Exam 17: Markov Processes44 Questionsadd course
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags
search iconSearch Question
flashcardsStudy Flashcards
Select questions type
  • Essay
  • Multiple Choice
  • Short Answer
  • True False
  • Matching
  • Select Tags

The linear programming model for crashing presented in the textbook assumes that any portion of the activity crash time can be achieved for a corresponding portion of the activity crashing cost.

Free
(True/False)
4.9/5
(28)
Question 1
Correct Answer:
Verified

True

Joseph King has ambitions to be mayor of Williston,North Dakota.Joe has determined the breakdown of the steps to the nomination and has estimated normal and crash costs and times for the campaign as follows (times are in weeks). Joseph King has ambitions to be mayor of Williston,North Dakota.Joe has determined the breakdown of the steps to the nomination and has estimated normal and crash costs and times for the campaign as follows (times are in weeks). 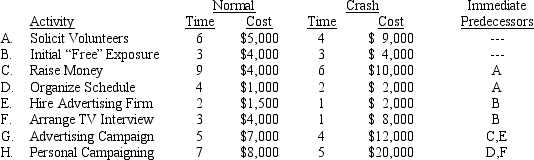Joe King is not a wealthy man and would like to organize a 16-week campaign at minimum cost.Write and solve a linear program to accomplish this task. Joe King is not a wealthy man and would like to organize a 16-week campaign at minimum cost.Write and solve a linear program to accomplish this task.

Free
(Essay)
4.7/5
(38)
Question 2
Correct Answer:
Verified

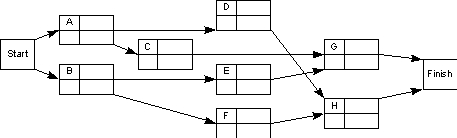
Define X<sub>i</sub> = earliest finish time for activity i Y<sub>i</sub> = the amount of time activity i is crashed MIN 2000Y<sub>A</sub>+2000Y<sub>C</sub>+500Y<sub>D</sub>+500Y<sub>E</sub>+2000Y<sub>F</sub>+5000Y<sub>G</sub>+6000Y<sub>H</sub> S.T.X<sub>A</sub> > 0 + (6 - Y<sub>A</sub>) X<sub>B</sub> > 0 + 3 X<sub>C</sub> > X<sub>A</sub> + (9 - Y<sub>C</sub>) X<sub>D</sub> > X<sub>A</sub> + (4 - Y<sub>D</sub>) X<sub>E</sub> > X<sub>B</sub> + (2 - Y<sub>E</sub>) X<sub>F</sub> > X<sub>B</sub> + (3 - Y<sub>F</sub>) X<sub>G</sub> < 16 X<sub>G</sub> > X<sub>C</sub> + (5 - Y<sub>G</sub>) X<sub>G</sub> > X<sub>E</sub> + (5 - Y<sub>G</sub>) X<sub>H</sub> > X<sub>D</sub> + (7 - Y<sub>H</sub>) X<sub>H</sub> > X<sub>F</sub> + (7 - Y<sub>H</sub>) X<sub>H</sub> < 16 Y<sub>A</sub> < 2 Y<sub>C</sub> < 3 Y<sub>D</sub> < 2 Y<sub>E</sub> < 1 Y<sub>F</sub> < 2 Y<sub>G</sub> < 1 Y<sub>H</sub> < 2 X<sub>i</sub>,Y<sub>j</sub> > 0 for all i
Define Xi = earliest finish time for activity i Yi = the amount of time activity i is crashed
MIN 2000YA+2000YC+500YD+500YE+2000YF+5000YG+6000YH
S.T.XA > 0 + (6 - YA)
XB > 0 + 3
XC > XA + (9 - YC)
XD > XA + (4 - YD)
XE > XB + (2 - YE)
XF > XB + (3 - YF)
XG < 16
XG > XC + (5 - YG)
XG > XE + (5 - YG)
XH > XD + (7 - YH)
XH > XF + (7 - YH)
XH < 16
YA < 2
YC < 3
YD < 2
YE < 1
YF < 2
YG < 1
YH < 2
Xi,Yj > 0 for all i

The project manager should monitor the progress of any activity with a large time variance even if the expected time does not identify the activity as a critical activity.

Free
(True/False)
4.8/5
(42)
Question 3
Correct Answer:
Verified

True

Activities with zero slack

(Multiple Choice)
5.0/5
(27)
Question 4

For the project represented below,determine the earliest and latest start and finish times for each activity as well as the expected overall completion time. For the project represented below,determine the earliest and latest start and finish times for each activity as well as the expected overall completion time. For the project represented below,determine the earliest and latest start and finish times for each activity as well as the expected overall completion time.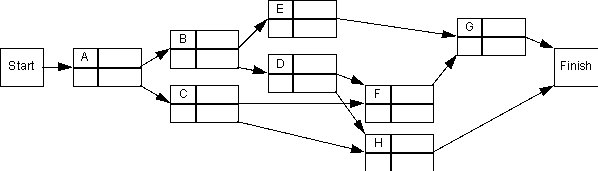

(Essay)
4.9/5
(30)
Question 5

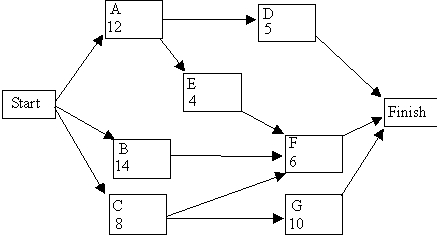
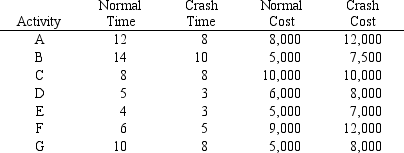The critical path for this network is A - E - F and the project completion time is 22 weeks. The critical path for this network is A - E - F and the project completion time is 22 weeks. If a deadline of 17 weeks is imposed,give the linear programming model for the crashing decision. The critical path for this network is A - E - F and the project completion time is 22 weeks. If a deadline of 17 weeks is imposed,give the linear programming model for the crashing decision. If a deadline of 17 weeks is imposed,give the linear programming model for the crashing decision.

(Essay)
4.9/5
(31)
Question 6

Critical activities are those that can be delayed without delaying the entire project.

(True/False)
4.8/5
(44)
Question 7

Constraints in the LP models for crashing decisions are required to compare the activity's earliest finish time with the earliest finish time of each predecessor.

(True/False)
4.9/5
(30)
Question 8

Slack equals

(Multiple Choice)
4.8/5
(38)
Question 9

The difference between an activity's earliest finish time and latest finish time equals the difference between its earliest start time and latest start time.

(True/False)
4.9/5
(32)
Question 10

Which is not a significant challenge of project scheduling?

(Multiple Choice)
4.9/5
(33)
Question 11

For an activity with more than one immediate successor activity,its latest-finish time is equal to the

(Multiple Choice)
4.9/5
(32)
Question 12

PERT and CPM are applicable only when there is no dependence among activities.

(True/False)
4.9/5
(35)
Question 13

A path through a project network must reach every node.

(True/False)
4.9/5
(27)
Question 14

A project consists of five activities.Naturally the paint mixing precedes the painting activities.Also,both ceiling painting and floor sanding must be done prior to floor buffing. A project consists of five activities.Naturally the paint mixing precedes the painting activities.Also,both ceiling painting and floor sanding must be done prior to floor buffing. a.Construct the PERT/CPM network for this problem. b.What is the expected completion time of this project? c.What is the probability that the project can be completed within 9 hr.? a.Construct the PERT/CPM network for this problem. b.What is the expected completion time of this project? c.What is the probability that the project can be completed within 9 hr.?

(Essay)
4.8/5
(32)
Question 15

For an activity with more than one immediate predecessor activity,which of the following is used to compute its earliest finish (EF)time?

(Multiple Choice)
4.7/5
(32)
Question 16

All activities on a critical path have zero slack time.

(True/False)
4.9/5
(39)
Question 17

It is possible to have more than one critical path at a time.

(True/False)
4.9/5
(36)
Question 18

Activities following a node

(Multiple Choice)
4.7/5
(32)
Question 19

The variance in the project completion time is the sum of the variances of all activities in the project.

(True/False)
4.9/5
(40)
Question 20
Showing 1 - 20 of 41
close modal

Filters

  • Essay(0)
  • Multiple Choice(0)
  • Short Answer(0)
  • True False(0)
  • Matching(0)