Exam 5: Discrete Probability Distributions

Exhibit 5-11 A local bottling company has determined the number of machine breakdowns per month and their respective probabilities as shown below: 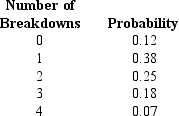-Refer to Exhibit 5-11. The probability of at least 3 breakdowns in a month is

Exhibit 5-1 The following represents the probability distribution for the daily demand of computers at a local store. 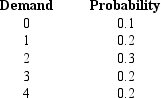-Refer to Exhibit 5-1. The expected daily demand is

Exhibit 5-3 Roth is a computer-consulting firm. The number of new clients that they have obtained each month has ranged from 0 to 6. The number of new clients has the probability distribution that is shown below. 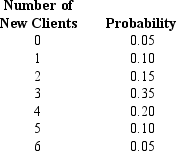-Refer to Exhibit 5-3. The variance is

Exhibit 5-7 The probability that Pete will catch fish when he goes fishing is .8. Pete is going to fish 3 days next week. Define the random variable X to be the number of days Pete catches fish. -Refer to Exhibit 5-7. The expected number of days Pete will catch fish is

Assume that you have a binomial experiment with p = 0.4 and a sample size of 50. The variance of this distribution is

The variance for the binomial probability distribution is

The random variable x has the following probability distribution: a.Is this probability distribution valid? Explain and list the requirements for a valid probability distribution. b.Calculate the expected value of x. c.Calculate the variance of x. d.Calculate the standard deviation of x.

For the following probability distribution: a.Determine E(x). b.Determine the variance and the standard deviation.

Four percent of the customers of a mortgage company default on their payments. A sample of five customers is selected. What is the probability that exactly two customers in the sample will default on their payments?

Exhibit 5-2 The student body of a large university consists of 60% female students. A random sample of 8 students is selected. -Refer to Exhibit 5-2. What is the probability that among the students in the sample exactly two are female?

Exhibit 5-10 The probability distribution for the number of goals the Lions soccer team makes per game is given below. 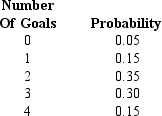-Refer to Exhibit 5-10. The expected number of goals per game is

Twenty-five percent of all resumes received by a corporation for a management position are from females. Fifteen resumes will be received tomorrow. a.What is the probability that exactly 5 of the resumes will be from females? b.What is the probability that fewer than 3 of the resumes will be from females? c.What is the expected number of resumes from women? d.What is the variance of the number of resumes from women?

Which of the following statements about a discrete random variable and its probability distribution are true?

Two percent of the parts produced by a machine are defective. Twenty parts are selected at random. Use the binomial probability tables to answer the following questions. a.What is the probability that exactly 3 parts will be defective? b.What is the probability that the number of defective parts will be more than 2 but fewer than 6? c.What is the probability that fewer than 4 parts will be defective? d.What is the expected number of defective parts? e. What is the variance for the number of defective parts?

Exhibit 5-7 The probability that Pete will catch fish when he goes fishing is .8. Pete is going to fish 3 days next week. Define the random variable X to be the number of days Pete catches fish. -Refer to Exhibit 5-7. The variance of the number of days Pete will catch fish is

Exhibit 5-5 Probability Distribution 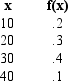-Refer to Exhibit 5-5. The expected value of x equals

The number of customers that enter a store during one day is an example of

Exhibit 5-8 The random variable x is the number of occurrences of an event over an interval of ten minutes. It can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length. It is known that the mean number of occurrences in ten minutes is 5.3. -Refer to Exhibit 5-8. The probability that there are 8 occurrences in ten minutes is

A production process produces 2% defective parts. A sample of five parts from the production process is selected. What is the probability that the sample contains exactly two defective parts?

When a particular machine is functioning properly, 80% of the items produced are non-defective. If three items are examined, what is the probability that one is defective? Use the binomial probability function to answer this question.