Exam 5: Discrete Probability Distributions

Exhibit 5-6 A sample of 2,500 people was asked how many cups of coffee they drink in the morning. You are given the following sample information. -Refer to Exhibit 5-6. The expected number of cups of coffee is

Twenty percent of the applications received for a particular position are rejected. What is the probability that among the next fourteen applications, a.none will be rejected? b.all will be rejected? c.less than 2 will be rejected? d.more than four will be rejected? e. Determine the expected number of rejected applications and its variance.

The hypergeometric probability distribution is identical to

Exhibit 5-4 Forty percent of all registered voters in a national election are female. A random sample of 5 voters is selected. -Refer to Exhibit 5-4. The probability that there are no females in the sample is

Exhibit 5-6 A sample of 2,500 people was asked how many cups of coffee they drink in the morning. You are given the following sample information. -Refer to Exhibit 5-6. The variance of the number of cups of coffee is

The number of electrical outages in a city varies from day to day. Assume that the number of electrical outages (x) in the city has the following probability distribution. The mean and the standard deviation for the number of electrical outages (respectively) are

A production process produces 2% defective parts. A sample of 5 parts from the production is selected. What is the probability that the sample contains exactly two defective parts? Use the binomial probability function and show your computations to answer this question.

Exhibit 5-3 Roth is a computer-consulting firm. The number of new clients that they have obtained each month has ranged from 0 to 6. The number of new clients has the probability distribution that is shown below. 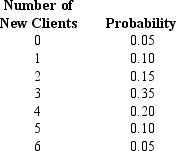-Refer to Exhibit 5-3. The expected number of new clients per month is

The records of a department store show that 20% of its customers who make a purchase return the merchandise in order to exchange it. In the next six purchases, a.what is the probability that three customers will return the merchandise for exchange? b.what is the probability that four customers will return the merchandise for exchange? c.what is the probability that none of the customers will return the merchandise for exchange?

In a large corporation, 65% of the employees are male. A random sample of five employees is selected. Use the Binomial probability tables to answer the following questions. a.What is the probability that the sample contains exactly three male employees? b.What is the probability that the sample contains no male employees? c.What is the probability that the sample contains more than three female employees? d.What is the expected number of female employees in the sample?

Exhibit 5-2 The student body of a large university consists of 60% female students. A random sample of 8 students is selected. -Refer to Exhibit 5-2. What is the probability that among the students in the sample at least 6 are male?

Exhibit 5-12 The police records of a metropolitan area kept over the past 300 days show the following number of fatal accidents. -Refer to Exhibit 5-12. What is the probability that in a given day there will be no accidents?

A random variable that can assume only a finite number of values is referred to as a(n)

A cosmetics salesperson, who calls potential customers to sell her products, has determined that 30% of her telephone calls result in a sale. Determine the probability distribution for her next three calls. Note that the next three calls could result in 0, 1, 2, or 3 sales.

In a binomial experiment

A description of the distribution of the values of a random variable and their associated probabilities is called a

A manufacturing company has 5 identical machines that produce nails. The probability that a machine will break down on any given day is .1. Define a random variable X to be the number of machines that will break down in a day. a.What is the appropriate probability distribution for X? Explain how X satisfies the properties of the distribution. b.Compute the probability that 4 machines will break down. c.Compute the probability that at least 4 machines will break down. d.What is the expected number of machines that will break down in a day? e. What is the variance of the number of machines that will break down in a day?

Exhibit 5-4 Forty percent of all registered voters in a national election are female. A random sample of 5 voters is selected. -Refer to Exhibit 5-4. The probability that the sample contains 2 female voters is

The expected value of a discrete random variable

Exhibit 5-8 The random variable x is the number of occurrences of an event over an interval of ten minutes. It can be assumed that the probability of an occurrence is the same in any two-time periods of an equal length. It is known that the mean number of occurrences in ten minutes is 5.3. -Refer to Exhibit 5-8. The probability that there are less than 3 occurrences is