Exam 20: The House Edge: Expected Values

A multiple choice exam offers four choices for each question. Paul just guesses the answers, so he has probability 1/4 of getting any one answer right. What is the expected number of right answers Paul will get if the test has 20 questions?

A friend rolls a cheap six-sided die many times. He reports that the probabilities of the possible outcomes are about as follows: Using the probabilities above, what is the expected outcome when rolling this die?

A game involving a pair of dice pays you $4 with probability 16/36, costs you $2 with probability 14/36, and costs you $6 with probability 6/36. What is your expected net result, in dollars, per play?

A game involving a pair of dice pays you $4 with probability 16/36, costs you $2 with probability 14/36, and costs you $6 with probability 6/36. If you play this game many times, in the long run how will your actual average gain per play compare with your answer to the previous question?

A children's cancer center sells 150 raffle tickets to raise money. Tickets cost $100 each. One ticket will be drawn at random for the $8,000 prize: a new men's Rolex watch. A second hospital is also conducting a benefit raffle to raise funds. They have 8000 tickets that also cost $100 each, and one ticket will be drawn at random also for a $350,000 prize-a new custom home. Which raffle has the best value for you per ticket?

A grocery chain runs a prize game by giving each customer a ticket that may win a prize when a box is scratched. Printed on the ticket are the following probabilities for a customer who shops once a week: 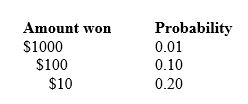If several thousand customers play the grocery store game, you expect that the mean amount they win will be close to

Kevin thinks he can use ESP to predict the outcome of rolling a fair die. You agree to pay him $3 if he can correctly predict the results of the next roll. Kevin has to pay you $1 if he is wrong. If Kevin doesn't have any psychic powers, which of the following is closest to the expected value of your net winnings on this bet?

Choose an American household at random and ask how many computers that household owns. Here are the probabilities as of 2009: 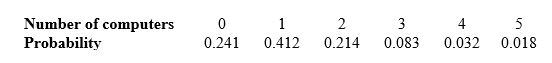What is the expected number of computers owned by a randomly chosen household?

A grocery chain runs a prize game by giving each customer a ticket that may win a prize when a box is scratched. Printed on the ticket are the following probabilities for a customer who shops once a week: 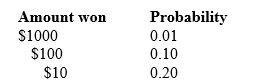What is the expected value of a customer's winnings in this game?

Consider the following lottery game. For this game, tickets cost $1, and there is a 10% chance of winning $5 (a net gain of $4). What is a player's expected net gain for each ticket that is bought for this game? (Note that a loss results in a net gain of "-$1").

Which of the following statements about a table of random digits is true?

Here is an assignment of probabilities to the face that comes up when rolling a die once: 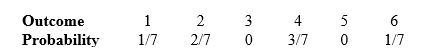What is the approximate expected outcome when rolling this die?

In government data, a family consists of two or more persons who live together and are related by blood or marriage. Choose an American family at random and count the number of people it contains. Here is the assignment of probabilities for your outcome: Using the probabilities above, what is the expected size of the family you draw?

Suppose you know the percentage of foul shots a basketball player makes during the season. You want to estimate the expected number of shots made in 10 shots. You simulate 10 shots 25 times and get the following numbers of shots made: 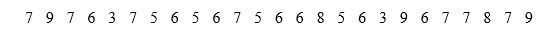Your estimate is:

An employee's office window overlooks a busy four-way stop, and the employee decides to track, per minute, the number of drivers who fail to stop. From data taken over many randomly selected times, the employee gets this probability model: 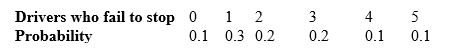The expected number of drivers failing to stop, per minute, is:

You play a game with two possible outcomes. Outcome A has probability 0.4 and outcome B has probability 0.6. When B occurs you win $2.00; otherwise, you lose $1.00. What is your expected value for this game?

A home game for a certain National League Central Division team is chosen at random. Here is the probability distribution for the number of hits the leadoff batter has had: What is the expected value of the number of hits the leadoff batter will have in a randomly chosen game?

An employee's office window overlooks a busy four-way stop, and the employee decides to track, per minute, the number of drivers who fail to stop. From data taken over many randomly selected times, the employee gets this probability model: 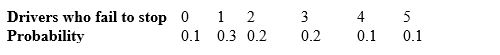In Question 14, the employee found the expected number of drivers failing to stop, per minute. The law of large numbers says:

An American household is chosen at random and asked how many tablet computers it owns. Here are the probabilities as determined by a recent survey: What is the expected number of tablet computers per household?

In many popular board games, a player rolls two dice and moves the number of spaces equal to the sum shown on the dice. Here is the assignment of probabilities to the sum of the numbers on the up faces when two dice are rolled: 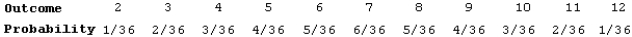Suppose you pay $5 to roll the two dice, and you'll win a dollar amount equal to the sum of the two dice. What is your expected profit for this game?