Exam 19: Simulation
Exam 1: Where Do Data Come From30 Questions
Exam 2: Samples, Good and Bad30 Questions
Exam 3: What Do Samples Tell Us55 Questions
Exam 4: Sample Surveys in the Real World36 Questions
Exam 5: Experiments, Good and Bad50 Questions
Exam 6: Experiments in the Real World32 Questions
Exam 7: Data Ethics21 Questions
Exam 8: Measuring33 Questions
Exam 9: Do the Numbers Make Sense25 Questions
Exam 10: Graphs, Good and Bad30 Questions
Exam 11: Displaying Distributions With Graphs22 Questions
Exam 13: Normal Distributions54 Questions
Exam 14: Describing Relationships: Scatterplots and Correlation56 Questions
Exam 15: Describing Relationships: Regression, Prediction, and Causation37 Questions
Exam 16: The Consumer Price Index and Government Statistics31 Questions
Exam 17: Thinking About Chance25 Questions
Exam 18: Probability Models30 Questions
Exam 19: Simulation20 Questions
Exam 20: The House Edge: Expected Values30 Questions
Exam 21: What Is a Confidence Interval43 Questions
Exam 22: What Is a Test of Significance30 Questions
Exam 23: Use and Abuse of Statistical Inference18 Questions
Exam 24: Two-Way Tables and the Chi-Square Test47 Questions
Select questions type
In a small Colombian village, 20 percent of the adults own a car, and 75 percent of the adults attend church regularly. Suppose that car ownership is independent of church attendance.
What is the probability that a randomly selected adult from this village does not own a car and does not attend church regularly?
Free
(Multiple Choice)
4.8/5  (38)
(38)
Correct Answer:
C
China has 1.36 billion people. Soft drink manufacturers work constantly to try to carve out a portion of that huge market. A Euromonitor study in 2014 showed that Coca-Cola held 63% of the entire Chinese soft drink market. A researcher wants to simulate choosing 10 Chinese soft-drink consumers at random and asking each if he or she purchases Coca-Cola.
One correct way to assign random digits to simulate the answer is
Free
(Multiple Choice)
4.9/5  (29)
(29)
Correct Answer:
C
Computer voice recognition software is getting better. Some companies claim that their software correctly recognizes 98% of all words spoken by a trained user.
The program recognizes words (or not) independently. To simulate the program's performance on 10 words, use two digits to simulate one word with 02 to 99 meaning "correct" and these random digits:
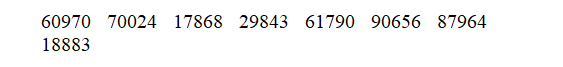 The number of words correct out of the 10 is
The number of words correct out of the 10 is
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
B
Suppose you toss a fair coin twenty-six times and each time you observe heads (i.e., 26 heads in a row). What is the probability of heads on your next toss?
(Multiple Choice)
4.8/5  (30)
(30)
China has 1.36 billion people. Soft drink manufacturers work constantly to try to carve out a portion of that huge market. A Euromonitor study in 2014 showed that Coca-Cola held 63% of the entire Chinese soft drink market. A researcher wants to simulate choosing 10 Chinese soft-drink consumers at random and asking each if he or she purchases Coca-Cola.
Use the correct assignment of digits from the previous question and the random digits below to simulate the answers of 10 Chinese citizens. Read across the row of random digits from left to right. How many of these 10 Chinese soft-drink consumers purchase Coca-Cola?
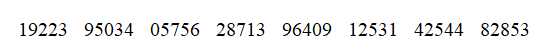
(Multiple Choice)
4.8/5  (41)
(41)
In a small Colombian village, 20 percent of the adults own a car, and 75 percent of the adults attend church regularly. Suppose that car ownership is independent of church attendance.
What is the probability that a randomly selected adult from this village owns a car and attends church regularly?
(Multiple Choice)
4.9/5  (30)
(30)
Suppose you toss a fair coin and roll a fair six-sided die. What is the probability your actions result in tails on the coin and 3 on the die?
(Multiple Choice)
4.8/5  (39)
(39)
Suppose we need to flip a coin, but we don't have one. However, we do have a random number table that we could use.
To simulate the outcome of tossing a coin you could assign random digits as follows:
(Multiple Choice)
4.9/5  (32)
(32)
A book about bridge says that the probability that each of the four players is dealt exactly one ace is about 0.11. To simulate an outcome with probability 0.11, a person could do which of the following simulations:
(Multiple Choice)
4.8/5  (31)
(31)
Suppose you toss a fair coin six times. What is the probability of all six tosses resulting in heads (i.e., you toss no tails)?
(Multiple Choice)
4.9/5  (31)
(31)
Bunches of bananas arriving from their supplier reach a grocer with probability 0.12 of being too ripe to sell. To simulate the event that a single bunch of bananas arriving at the grocery is too ripe to sell, the produce manager could use two digits from a random generator with the convention (choose the best answer):
(Multiple Choice)
4.8/5  (33)
(33)
I want to use simulation to estimate the probability of getting exactly one head and one tail in two tosses of a fair coin. I assign the digits 0, 1, 2, 3, 4 to heads and 5, 6, 7, 8, 9 to tails. Using the following random digits to simulate, what is the estimate of the probability?
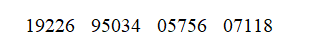
(Multiple Choice)
4.8/5  (37)
(37)
The WNBA player Temeka Johnson of the Los Angeles Sparks (2015) is a career 82 percent free-throw shooter. Suppose Tameka is fouled while attempting a three-point shot so she is awarded three free throws. What is the probability that she will make all three of her free throws?
(Multiple Choice)
4.9/5  (39)
(39)
A multiple choice exam offers four choices for each question. Jason just guesses the answers, so he has probability 1/4 of getting any one answer right. You want to simulate whether Jason's answers to 10 questions are right or wrong. One correct way to do this is
(Multiple Choice)
5.0/5  (32)
(32)
Suppose flights at a large metropolitan airport are on-time 68% of the time and late 32% of the time. We want to use a table of random digits to simulate flight status (on-time or late), so we'll assign 01, 02, … , 68 to represent on-time flights, and 69, 70, … , 99, 00 to represent late flights.
You want to estimate the probability that 15 or more flights out of 20 will be on-time at this airport. You simulate 20 flights 25 times and get the following numbers of on-time flights:
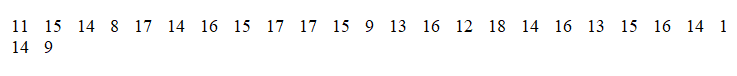 What is your estimate of the probability?
What is your estimate of the probability?
(Multiple Choice)
4.9/5  (33)
(33)
Suppose you roll three fair six-sided dice. What is the probability of each die showing an even number (i.e., you roll no odd numbers)?
(Multiple Choice)
4.9/5  (36)
(36)
Computer voice recognition software is getting better. Some companies claim that their software correctly recognizes 98% of all words spoken by a trained user.
To simulate recognizing a single word when the probability of being correct is 0.98, you could use random digits as follows:
(Multiple Choice)
4.9/5  (32)
(32)
Suppose flights at a large metropolitan airport are on-time 68% of the time and late 32% of the time. We want to use a table of random digits to simulate flight status (on-time or late), so we'll assign 01, 02, … , 68 to represent on-time flights, and 69, 70, … , 99, 00 to represent late flights.
Use the information above and these random digits to simulate 20 flights at this airport:
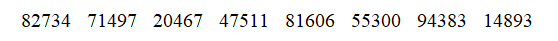 How many of the simulated flights were on-time?
How many of the simulated flights were on-time?
(Multiple Choice)
4.8/5  (43)
(43)
A researcher estimates that 30 percent of students at his college would be willing to pay for Google Fiber, the high-speed, superfast Internet access. The researcher chooses a student at random and asks that student if she would pay. To simulate the outcome, the researcher could use one random digit as follows:
(Multiple Choice)
4.9/5  (34)
(34)
In a small Colombian village, 20 percent of the adults own a car, and 75 percent of the adults attend church regularly. Suppose that car ownership is independent of church attendance.
What is the probability that a randomly selected adult from this village owns a car but does not attend church regularly?
(Multiple Choice)
5.0/5  (35)
(35)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)