Exam 8: Graphs of the Trigonometric Functions
Exam 1: Fundamentals25 Questions
Exam 2: Equations and Inequalities24 Questions
Exam 3: Functions24 Questions
Exam 4: Polynomial and Rational Functions Applications to Optimization25 Questions
Exam 5: Exponential and Logarithmic Functions24 Questions
Exam 6: An Introduction to Trigonometry Via Right Triangles25 Questions
Exam 7: The Trigonometric Functions25 Questions
Exam 8: Graphs of the Trigonometric Functions25 Questions
Exam 9: Analytical Trigonometry25 Questions
Exam 10: Additional Topics in Trigonometry25 Questions
Exam 11: Systems of Equations25 Questions
Exam 12: The Conic Sections25 Questions
Exam 13: Roots of Polynomial Equations25 Questions
Exam 14: Additional Topics in Algebra25 Questions
Select questions type
Consider the function . Specify the period.
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
D
Graph the function for one period, and show (or specify) intercepts and asymptotes.
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
C
Consider the function on the interval . Determine the -intercepts by giving the -coordinate(s).
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
B
State whether the function is increasing or decreasing on the interval.
(Multiple Choice)
4.8/5  (35)
(35)
Graph the function for one period, and show (or specify) the intercepts and the asymptotes.
(Multiple Choice)
4.9/5  (30)
(30)
Graph the function for one period, and show (or specify) intercepts and asymptotes.
(Multiple Choice)
4.8/5  (37)
(37)
Graph the function for one period, and show (or specify) the intercepts and the asymptotes.
(Multiple Choice)
4.9/5  (29)
(29)
Consider the function on the interval . Specify the intervals in which the function is increasing.
(Multiple Choice)
4.8/5  (37)
(37)
State whether the function is increasing or decreasing on the interval.
(Multiple Choice)
4.7/5  (38)
(38)
Refer to the graph of in the figure. Specify the coordinates of the point I. 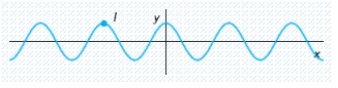
(Multiple Choice)
4.9/5  (34)
(34)
Refer to the graph of in the figure. Specify the coordinates of the point I. 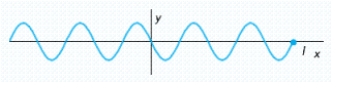
(Multiple Choice)
4.8/5  (40)
(40)
Graph the function for one period, and show (or specify) intercepts and asymptotes.
(Multiple Choice)
4.9/5  (32)
(32)
Determine whether the equation for the graph has the form or ( with ) and then find the values of and . 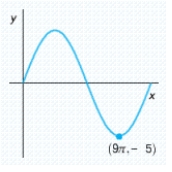
(Multiple Choice)
4.7/5  (33)
(33)
Consider the function on the interval . Determine the -intercepts by giving the -coordinate(s).
(Multiple Choice)
4.8/5  (35)
(35)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)