Exam 10: Additional Topics in Trigonometry
Exam 1: Fundamentals25 Questions
Exam 2: Equations and Inequalities24 Questions
Exam 3: Functions24 Questions
Exam 4: Polynomial and Rational Functions Applications to Optimization25 Questions
Exam 5: Exponential and Logarithmic Functions24 Questions
Exam 6: An Introduction to Trigonometry Via Right Triangles25 Questions
Exam 7: The Trigonometric Functions25 Questions
Exam 8: Graphs of the Trigonometric Functions25 Questions
Exam 9: Analytical Trigonometry25 Questions
Exam 10: Additional Topics in Trigonometry25 Questions
Exam 11: Systems of Equations25 Questions
Exam 12: The Conic Sections25 Questions
Exam 13: Roots of Polynomial Equations25 Questions
Exam 14: Additional Topics in Algebra25 Questions
Select questions type
Determine the graph that reflects the polar equation.
Free
(Multiple Choice)
4.7/5  (33)
(33)
Correct Answer:
A
Assume that the vectors , , and are defined as follows:
Compute
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
A
Convert the given rectangular coordinates to polar coordinates. Express the answer in such a way that r is nonnegative and .
Free
(Multiple Choice)
4.8/5  (45)
(45)
Correct Answer:
B
The accompanying figure shows two ships at points and , which are in the same vertical plane as an airplane at point . When the height of the airplane is 4,000 ft, the angle of depression to is 38° and that to is 15°. Find the distance between the two ships. 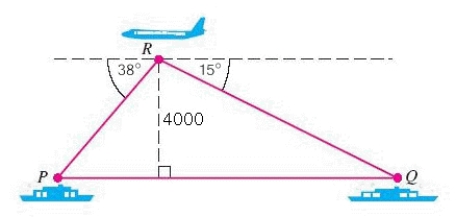
(Multiple Choice)
4.8/5  (37)
(37)
Use the equation to determine polar coordinates of the point B. 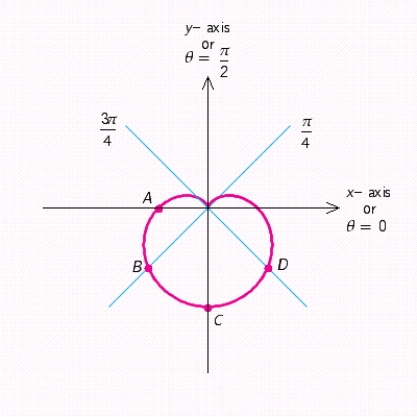
(Multiple Choice)
5.0/5  (43)
(43)
The initial point for the vector is the origin, and denotes the angle (measured counterclockwise) from the -axis to the vector. The magnitude of is cm/sec, and Compute the horizontal and vertical components of the given vector. (Round your answers to two decimal places.)
(Multiple Choice)
4.9/5  (36)
(36)
An airplane crashes in a lake and is spotted by observers at lighthouses A and B along the coast. Lighthouse B is 1.10 miles due east of lighthouse A. The bearing of the airplane from lighthouse A is ; the bearing of the plane from lighthouse B is . Find the distance from each lighthouse to the crash site.
(Multiple Choice)
4.9/5  (32)
(32)
Convert the given rectangular coordinates to polar coordinates. Express the answer in such a way that r is nonnegative and .
(Multiple Choice)
4.8/5  (34)
(34)
Convert from rectangular to trigonometric form. (Choose an argument such that .)
(Multiple Choice)
4.9/5  (33)
(33)
Determine the graph that reflects the polar equation. (five-leafed rose)
(Multiple Choice)
4.8/5  (37)
(37)
Two points P and Q are on opposite sides of a river (see the sketch). From P to another point R on the same side is 340 ft. Angles and are found to be and , respectively. Compute the distance from P to Q, across the river. (Round your answer to the nearest foot.) 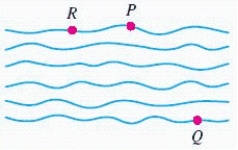
(Multiple Choice)
4.9/5  (41)
(41)
Assume that the vectors , , and are defined as follows: Compute .
(Multiple Choice)
4.8/5  (24)
(24)
Convert from rectangular to trigonometric form. (Choose an argument such that .) 6
(Multiple Choice)
5.0/5  (39)
(39)
Use the given information to find the cosines of angles in . cm, cm, cm
(Multiple Choice)
4.8/5  (33)
(33)
On a sheet of paper, graph the parametric equation after eliminating the parameter ). Specify the approximate direction on the curve corresponding to increasing values of .
(Multiple Choice)
4.8/5  (25)
(25)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)