Exam 6: An Introduction to Trigonometry Via Right Triangles
Exam 1: Fundamentals25 Questions
Exam 2: Equations and Inequalities24 Questions
Exam 3: Functions24 Questions
Exam 4: Polynomial and Rational Functions Applications to Optimization25 Questions
Exam 5: Exponential and Logarithmic Functions24 Questions
Exam 6: An Introduction to Trigonometry Via Right Triangles25 Questions
Exam 7: The Trigonometric Functions25 Questions
Exam 8: Graphs of the Trigonometric Functions25 Questions
Exam 9: Analytical Trigonometry25 Questions
Exam 10: Additional Topics in Trigonometry25 Questions
Exam 11: Systems of Equations25 Questions
Exam 12: The Conic Sections25 Questions
Exam 13: Roots of Polynomial Equations25 Questions
Exam 14: Additional Topics in Algebra25 Questions
Select questions type
Use the following information to determine the remaining five trigonometric values. Rationalize any denominators that contain radicals.
Free
(Multiple Choice)
4.9/5  (25)
(25)
Correct Answer:
A
Use the definitions (not a calculator) to evaluate the six trigonometric functions of the angle.
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
E
Find the area of the triangle. Use a calculator and round your final answer to two decimal places. 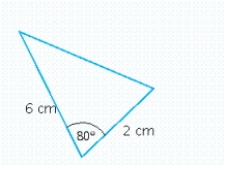
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
B
Evaluate the expression using the concept of a reference angle.
(Multiple Choice)
4.9/5  (41)
(41)
Use the definitions to evaluate the six trigonometric functions of . In cases in which a radical occurs in a denominator, rationalize the denominator. 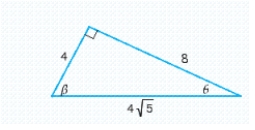
(Multiple Choice)
4.9/5  (36)
(36)
Use the following information to express the remaining five trigonometric values as functions of . Assume that is positive. Rationalize any denominators that contain radicals.
(Multiple Choice)
4.9/5  (35)
(35)
From a point on ground level, you measure the angle of elevation to the top of a mountain to be . Then you walk farther away from the mountain and find that the angle of elevation is now . Find the height of the mountain.
(Multiple Choice)
4.8/5  (27)
(27)
Use the following formation to determine the remaining five trigonometric values. Rationalize any denominators that contain radicals.
(Multiple Choice)
4.8/5  (37)
(37)
Use the definitions (not a calculator) to evaluate the six trigonometric functions of the angle.
(Multiple Choice)
5.0/5  (34)
(34)
The accompanying figure shows two ships at points and , which are in the same vertical plane as an airplane at point . When the height of the airplane is , the angle of depression to is and that to is .Find the distance between the two ships. 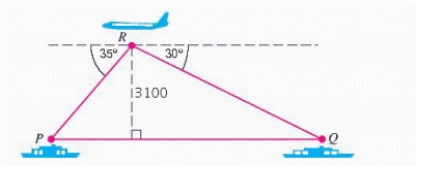
(Multiple Choice)
4.8/5  (30)
(30)
Use the definitions (not a calculator) to evaluate the six trigonometric functions of the angle.
(Multiple Choice)
4.9/5  (38)
(38)
Suppose that is a right triangle with . If and , find the quantities.
(Multiple Choice)
4.7/5  (35)
(35)
The radius of the circle in the figure is 2 units. Express the length in terms of . 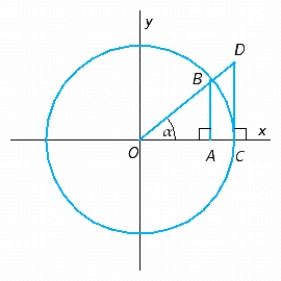
(Multiple Choice)
4.8/5  (35)
(35)
Evaluate the expression using the concept of a reference angle.
(Multiple Choice)
4.8/5  (45)
(45)
Use the following information to express the remaining five trigonometric values as functions of . Assume that is positive. Rationalize any denominators that contain radicals.
(Multiple Choice)
4.8/5  (42)
(42)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)