Exam 8: Systems of Equations and Inequalities
Exam 1: Topics From Algebra25 Questions
Exam 2: Functions and Graphs24 Questions
Exam 3: Polynomial and Rational Functions24 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions24 Questions
Exam 5: Trigonometric Functions25 Questions
Exam 6: Analytic Trigonometry25 Questions
Exam 7: Applications of Trigonometry25 Questions
Exam 8: Systems of Equations and Inequalities25 Questions
Exam 9: Sequences, Series, and Probability25 Questions
Exam 10: Topics From Analytical Geometry25 Questions
Select questions type
Find the maximum and minimum values of the objective function on the region in the figure. 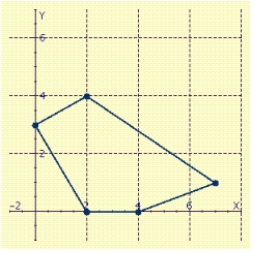
Free
(Multiple Choice)
4.7/5  (31)
(31)
Correct Answer:
E
Use the method of substitution to solve the system.
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
B
A shop specializes in preparing blends of gourmet coffees. From Colombian, Costa Rican, and Kenyan coffees, the owner wishes to prepare 3-pounds bags that will sell for $8.50. The cost per pound of these coffees is $10, $6, and $8, respectively. The amount of Colombian is to be three times the amount of Costa Rican. Find the amount of each type of coffee in the blend.
(Multiple Choice)
4.9/5  (36)
(36)
Let be the identity matrix of order 2, and let . Find the polynomial for the given matrix A in order to find the zeros of .
(In the study of matrices, is the characteristic polynomial of A, and the zeros of are the characteristic values (eigenvalues) of A.)
(Multiple Choice)
4.8/5  (38)
(38)
Find the determinant of the matrix after introducing zeros.
(Multiple Choice)
4.9/5  (32)
(32)
A hospital dietician wishes to prepare a corn-squash vegetable dish that will provide at least grams of protein and cost no more than cents per serving. An ounce of creamed corn provides gram of protein and costs cents. An ounce of squash supplies gram of protein and costs cents. For taste, there must be at least ounces of corn and at least as much squash as corn. It is important to keep the total number of ounces in a serving as small as possible. Find the combination of corn and squash that will minimize the amount of ingredients used per serving.
(Multiple Choice)
4.7/5  (24)
(24)
The data in the table are generated by the function . Approximate the unknown constants a and b to four decimal places. x
1 2 3 4
F ( x )
0)71939 0.41687 0.24157 0.13998
(Multiple Choice)
4.9/5  (43)
(43)
A manufacturer of tennis rackets makes a profit of $15 on each oversized racket and $10 on each standard racket. To meet dealer demand, daily production of standard rackets should be between 25 and 75, and production of oversized rackets should be between 8 and 27. To maintain high quality, the total number of rackets produced should not exceed 75 per day. How many of each type should be manufactured daily to maximize the profit?
(Multiple Choice)
4.8/5  (32)
(32)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)