Exam 6: Analytic Trigonometry
Exam 1: Topics From Algebra25 Questions
Exam 2: Functions and Graphs24 Questions
Exam 3: Polynomial and Rational Functions24 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions24 Questions
Exam 5: Trigonometric Functions25 Questions
Exam 6: Analytic Trigonometry25 Questions
Exam 7: Applications of Trigonometry25 Questions
Exam 8: Systems of Equations and Inequalities25 Questions
Exam 9: Sequences, Series, and Probability25 Questions
Exam 10: Topics From Analytical Geometry25 Questions
Select questions type
Use an addition or subtraction formula to find the solutions of the equation that are in the interval .
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
A
Find the solutions of the equation that are in the interval
(Multiple Choice)
4.7/5  (28)
(28)
A golfer, centered in a b = 40-yard-wide straight fairway, hits a ball a = 230 yards. Approximate the largest angle the drive can have from the center of the fairway if the ball is to stay in the fairway (see the figure). Round the answer to the nearest hundredth. 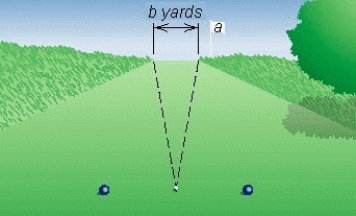
(Multiple Choice)
4.9/5  (33)
(33)
Use the graph of f to find the simplest expression g(x) such that the equation f (x) = g (x) is an identity. 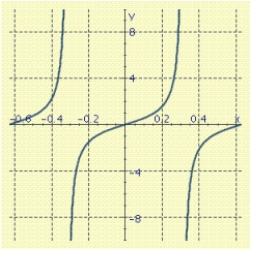
(Multiple Choice)
4.7/5  (29)
(29)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)