Exam 10: Topics From Analytical Geometry
Exam 1: Topics From Algebra25 Questions
Exam 2: Functions and Graphs24 Questions
Exam 3: Polynomial and Rational Functions24 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions24 Questions
Exam 5: Trigonometric Functions25 Questions
Exam 6: Analytic Trigonometry25 Questions
Exam 7: Applications of Trigonometry25 Questions
Exam 8: Systems of Equations and Inequalities25 Questions
Exam 9: Sequences, Series, and Probability25 Questions
Exam 10: Topics From Analytical Geometry25 Questions
Select questions type
Find a polar equation in r and that has the same graph as the equation in x and y.
Free
(Multiple Choice)
4.8/5  (24)
(24)
Correct Answer:
B
Find a polar equation of the conic with focus at the pole that has the eccentricity and equation of directrix.
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
A
An arch of a bridge is semi-elliptical, with major axis horizontal. The base of the arch is 30 feet across, and the highest part of the arch is 10 feet above the horizontal roadway, as shown in the figure. Find the height of the arch 7 feet from the center of the base. 
Free
(Multiple Choice)
5.0/5  (34)
(34)
Correct Answer:
B
Find an equation for the ellipse that has its center at the origin and satisfies the conditions.
(Multiple Choice)
4.9/5  (33)
(33)
Find a polar equation in r and that has the same graph as the equation in x and y.
(Multiple Choice)
4.8/5  (28)
(28)
Find a polar equation in r and that has the same graph as the equation in x and y.
(Multiple Choice)
4.8/5  (37)
(37)
Polar equations of conics can be used to describe the motion of comets. These paths can be graphed using the following polar equation, where e is the eccentricity of the conic and r per is the perihelion distance measured in AU. For Encke's Comet r per = 0.3317 and e = 0.8499, determine whether its trajectory is elliptical, parabolic, or hyperbolic.
(Multiple Choice)
4.9/5  (34)
(34)
Find an equation of the parabola that satisfies the condition. Vertex , focus
(Multiple Choice)
4.8/5  (45)
(45)
Find an equation for the parabola that has a horizontal axis and passes through the given points.
(Multiple Choice)
4.8/5  (30)
(30)
Find a polar equation of the conic with focus at the pole that has the eccentricity and equation of directrix. ,
(Multiple Choice)
4.8/5  (32)
(32)
Find a polar equation in r and 0 of the parabola with focus at the pole and the given vertex.
(Multiple Choice)
4.8/5  (34)
(34)
Find a polar equation in r and 0 of the parabola with focus at the pole and the given vertex.
(Multiple Choice)
4.8/5  (34)
(34)
Shown in the figure is the Lissajous figure given by Find the period of the figure - that is, the length of the smallest t-interval that traces the curve. 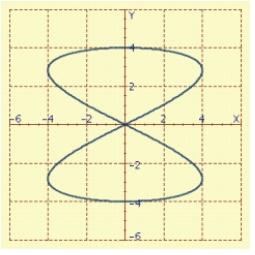
(Multiple Choice)
4.8/5  (40)
(40)
Lissajous figures are used in the study of electrical circuits to determine the phase difference between a known voltage and an unknown voltage
having the same frequency. The voltages are graphed parametrically as and . If is acute, then where y int is the nonnegative y -intercept and y max is the maximum y -value on the curve. Graph the parametric curve and use the graph to approximate in degrees if (t)=40(60\pit),(t)=90(60\pit-\pi/3), 0\leqt\leq0.035
(Multiple Choice)
4.9/5  (33)
(33)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)