Exam 5: Trigonometric Functions
Exam 1: Topics From Algebra25 Questions
Exam 2: Functions and Graphs24 Questions
Exam 3: Polynomial and Rational Functions24 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions24 Questions
Exam 5: Trigonometric Functions25 Questions
Exam 6: Analytic Trigonometry25 Questions
Exam 7: Applications of Trigonometry25 Questions
Exam 8: Systems of Equations and Inequalities25 Questions
Exam 9: Sequences, Series, and Probability25 Questions
Exam 10: Topics From Analytical Geometry25 Questions
Select questions type
Scientists sometimes use the formula to simulate temperature variations during the day, with time t in hours, temperature f ( t ) in , and t=0 corresponding to midnight. Assume that f ( t ) is decreasing at midnight. Determine values of a, b, c, and d that fit the information: the high temperature is 19 , and the low temperature of -19 occurs at 4 A.M.
Free
(Multiple Choice)
4.7/5  (33)
(33)
Correct Answer:
E
An airplane flying at a speed of 300 mi/hr flies from a point A in the direction for 15 minutes and then flies in the direction for 45 minutes. Approximate, to the nearest mile, the distance from the airplane to A.
Free
(Multiple Choice)
4.8/5  (23)
(23)
Correct Answer:
B
The graph of an equation of a sine wave is shown in the figure. Find the amplitude, period, and phase shift. 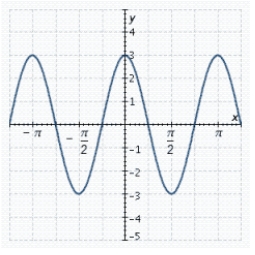
(Multiple Choice)
4.9/5  (34)
(34)
The phases of the moon can be described using the phase angle , determined by the sun, the moon, and the Earth, as shown in the figure. Because the moon orbits Earth, changes during the course of a month. The area of the region A of the moon, which appears illuminated to an observer on Earth, is given by , where R = 1,080 mi is the radius of the moon. Approximate A for the following position of the moon: 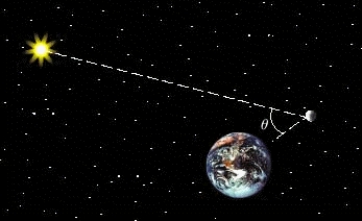
(Multiple Choice)
4.8/5  (40)
(40)
The thickness of the ozone layer can be estimated using the formula where I 0 is the intensity of a particular wavelength of light from the sun before it reaches the atmosphere, I is the intensity of the same wavelength after passing through a layer of ozone x centimeters thick, k is the absorption constant of ozone for that wavelength, and is the acute angle that the sunlight makes with the vertical. Suppose that for a wavelength of 3,055 10 - 8 centimeter with k 1.93, I o /I is measured as 1.72 and . Approximate the thickness of the ozone layer to the nearest 0.01 centimeter.
(Multiple Choice)
4.9/5  (37)
(37)
A rocket is fired at sea level and climbs at a constant angle of through a distance of 10,500 feet. Approximate its altitude to the nearest foot.
(Multiple Choice)
4.9/5  (38)
(38)
A builder wishes to construct a ramp 23 feet long that rises to a height of 4.5 feet above level ground. Approximate the angle that the ramp should make with the horizontal. Round the answer to the nearest degree.
(Multiple Choice)
4.8/5  (36)
(36)
Find an equation using the cotangent function that has the same graph as .
(Multiple Choice)
4.9/5  (35)
(35)
Find the exact values of the six trigonometric functions of the angle, whenever possible.
(Multiple Choice)
4.7/5  (33)
(33)
Rewrite the expression in nonradical form without using absolute values for the indicated values of . ;
(Multiple Choice)
4.7/5  (26)
(26)
A CB antenna is located on the top of a garage that is 17 feet tall. From a point on level ground that is 120 feet from a point directly below the antenna, the antenna subtends an angle of , as shown in the figure. Approximate the length of the antenna. Give the answer to one decimal place. 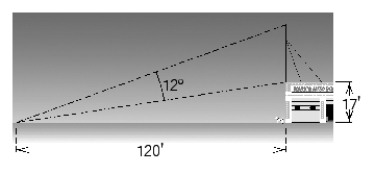
(Multiple Choice)
4.8/5  (39)
(39)
A ladder 24 feet long leans against the side of a building, and the angle between the ladder and the building is .
a) Approximate the distance from the bottom of the ladder to the building. Give the answer to one decimal place.
b) If the distance from the bottom of the ladder to the building is increased by 2 feet, approximately how far does the top of the ladder move down the building? Give the answer to one decimal place.
(Multiple Choice)
4.8/5  (40)
(40)
Express the angle as a decimal, to the nearest ten-thousandth of a degree.
(Multiple Choice)
4.8/5  (36)
(36)
Points on the terminal sides of angles play an important part in the design of arms for robots. Suppose a robot has a straight arm 20 inches long that can rotate about the origin in a coordinate plane. If the robot's hand is located at (20, 0) and then rotates through an angle of 60 o , what is the new location of the hand?
(Multiple Choice)
4.8/5  (33)
(33)
A forester, 210 feet from the base of a redwood tree, observes that the angle between the ground and the top of the tree is . Estimate the height of the tree.
(Multiple Choice)
4.8/5  (33)
(33)
Showing 1 - 20 of 25
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)