Exam 3: Polynomial and Rational Functions
Exam 1: Topics From Algebra25 Questions
Exam 2: Functions and Graphs24 Questions
Exam 3: Polynomial and Rational Functions24 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions24 Questions
Exam 5: Trigonometric Functions25 Questions
Exam 6: Analytic Trigonometry25 Questions
Exam 7: Applications of Trigonometry25 Questions
Exam 8: Systems of Equations and Inequalities25 Questions
Exam 9: Sequences, Series, and Probability25 Questions
Exam 10: Topics From Analytical Geometry25 Questions
Select questions type
A polynomial f ( x ) with real coefficients and leading coefficient 1 has the given zeros and degree. Express f ( x ) as a product of linear and quadratic polynomials with real coefficients that are irreducible over R.
Free
(Multiple Choice)
4.8/5  (33)
(33)
Correct Answer:
A
Salt water of concentration 0.5 pound of salt per gallon flows into a large tank that initially contains 220 gallons of pure water. If the flow rate of salt water into the tank is 4 gal/min, find a formula for the salt concentration (in lb/gal) after t minutes.
Free
(Multiple Choice)
4.7/5  (26)
(26)
Correct Answer:
C
Use synthetic division to decide whether is a zero of the equation. ;
Free
(Multiple Choice)
4.8/5  (29)
(29)
Correct Answer:
A
The pressure P acting at a point in a liquid is directly proportional to the distance d from the surface of the liquid to the point. Express P as a function of d by means of a formula that involves a constant of proportionality k. In a certain oil tank, the pressure at a depth of 8 feet is 472. Find the value of k.
(Multiple Choice)
4.7/5  (29)
(29)
The density D(h) (in kg/m 3 ) of the earth's atmosphere at an altitude of h meters can be approximated by where and . Use a graphing utility to graph D and approximate the altitude h at which the density is 0.3.
(Multiple Choice)
4.9/5  (29)
(29)
Find the fourth-degree polynomial function whose graph is shown in the figure. 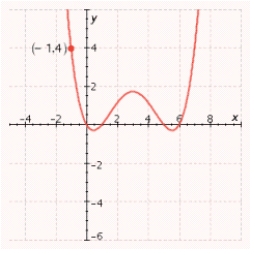
(Multiple Choice)
4.9/5  (37)
(37)
Poiseuille's law states that the blood flow rate F ( in L/min ) through a major artery is directly proportional to the product of the fourth power of the radius r and the blood pressure P. During heavy exercise, normal blood flow rates sometimes triple. If the radius of a major artery increases by 7%, approximately how much harder must the heart pump?
(Multiple Choice)
4.8/5  (33)
(33)
Find a factored form with integer coefficients of the polynomial f shown in the figure. 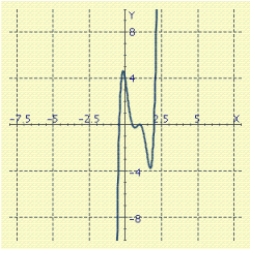
(Multiple Choice)
4.8/5  (29)
(29)
A canvas camping tent is to be constructed in the shape of a pyramid with a square base. An 8-foot pole will form the center support, as illustrated in the figure. Find the length x of a side of the base so that the total amount of canvas needed for the sides and bottom is 384 ft 2 . 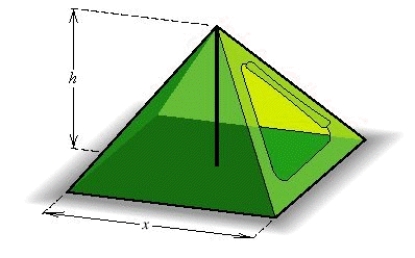
(Multiple Choice)
4.9/5  (28)
(28)
Express the statement as a formula that involves the variables w, z, u and a constant of proportionality k, and then determine the value of k from the condition : w varies directly as z and inversely as the square root of u, if z = 3 and u = 4, then w = 18
(Multiple Choice)
4.9/5  (34)
(34)
Express the statement as a formula that involves the variables q, x, y and a constant of proportionality k, and then determine the value of k from the condition : q is inversely proportional to the sum of x and y, if x = 2.5 and y = 3.6, then q = 3.8
(Multiple Choice)
4.8/5  (38)
(38)
When uranium disintegrates into lead, one step in the process is the radioactive decay of radium into radon gas. Radon enters through the soil into home basements, where it presents a health hazard if inhaled. In the simplest case of radon detection, a sample of air with volume V is taken. After equilibrium has been established, the radioactive decay D of the radon gas is counted with efficiency E over time t. The radon concentration C present in the sample of air varies directly as the product of D and E and inversely as the product of V and t. For a fixed radon concentration C and time t, find the change in the radioactive decay count D if V is multiplied by 2 and E is reduced by 14%.
(Multiple Choice)
4.9/5  (35)
(35)
A polynomial f ( x ) with real coefficients and leading coefficient 1 has the given zero and degree. Express f ( x ) as a product of linear and quadratic polynomials with real coefficients that are irreducible over R.
(Multiple Choice)
4.8/5  (37)
(37)
From a rectangular piece of cardboard having dimensions W = 18 and L = 40 an open box is to be made by cutting out identical squares of area x 2 from each corner and turning up the sides (see Illustration). Find all positive values of x such that the volume of the box V ( x ) > 0. Include only allowable values of x in your answer. 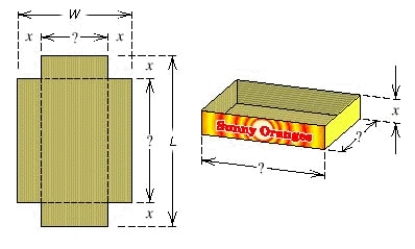
(Multiple Choice)
4.8/5  (36)
(36)
Showing 1 - 20 of 24
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)