Exam 6: The Definite Integral
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
Find all antiderivatives of the function.
-f(x) = Enter your answer with any fractional coefficients and powers in reduced form .
(Short Answer)
4.9/5  (36)
(36)
In the figure below, the region enclosed by the curves y = - , y = -x, and y = -x + 3 is shown. Set up an integral or sum of integrals to find the area of the shaded region. (Do not calculate the area.) 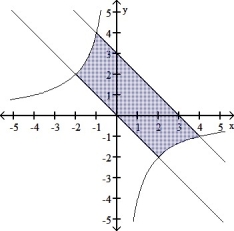
(Multiple Choice)
4.8/5  (44)
(44)
Find the area of the region bounded by y = 4x - and the x-axis.
Enter a reduced fraction of form .
(Short Answer)
4.8/5  (27)
(27)
Enter your answer as a(b + ) with any fractions in reduced form .
(Short Answer)
4.9/5  (37)
(37)
What is the area under the curve y = + x from x = 1 to x = 2?
(Multiple Choice)
5.0/5  (33)
(33)
A region is bounded above by the graph of y = and below by the x-axis on the interval from to x = 3. Find the volume of the solid of revolution generated by revolving the region about the x-axis.
Enter your answer as a reduced quotient of form .
(Short Answer)
4.8/5  (29)
(29)
Find: Enter your answer as a power function in x in standard form with any fractional coefficients or powers in reduced form and any constant at the right end.
(Short Answer)
4.9/5  (41)
(41)
A region is bounded by the graph of y = , the y-axis, and the horizontal line . Find the volume of the solid of revolution generated by revolving the region about the x-axis.
Enter your answer as a reduced quotient in form .
(Short Answer)
4.8/5  (29)
(29)
Find: Enter your answer as a polynomial in x in standard form with any fractional coefficients or powers reduced of form .
(Short Answer)
4.8/5  (38)
(38)
Find the area of the region bounded by y =1 - 2x - and the lines x = -1 and x = 0.
Enter a reduced fraction of form .
(Short Answer)
4.7/5  (37)
(37)
Find the area of the region bounded by the curve f(x) = 5x - 2 and the line y = 3.
Enter just a reduced fraction of form .
(Short Answer)
4.8/5  (43)
(43)
Suppose that the marginal revenue for a retailer is 6 - + x dollars at sales level x. If 4 units are currently being sold, what is the extra revenue received from the sale of 5 additional units?
(Multiple Choice)
4.8/5  (44)
(44)
A helicopter rises straight up in the air so that its velocity t seconds after take-off is feet per second. If the landing pad is 100 feet above the ground, which of the following gives the height of the helicopter at time t ?
(Multiple Choice)
4.9/5  (39)
(39)
Showing 121 - 135 of 135
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)