Exam 12: Probability and Calculus
Exam 1: The Derivative189 Questions
Exam 2: Applications of the Derivative93 Questions
Exam 3: Techniques of Differentiation69 Questions
Exam 4: Logarithm Functions135 Questions
Exam 5: Applications of the Exponential and Natural Logarithm Functions73 Questions
Exam 6: The Definite Integral135 Questions
Exam 7: Functions of Several Variables119 Questions
Exam 8: The Trigonometric Functions128 Questions
Exam 9: Techniques of Integration178 Questions
Exam 10: Differential Equations126 Questions
Exam 11: Taylor Polynomials and Infinite Series132 Questions
Exam 12: Probability and Calculus92 Questions
Select questions type
The table below is the probability table for a random variable X. Find the standard deviation of X. Outcome -3 -2 -1 1 2 3 Probability 0.1 0.1 0.4 0.3 0.05 0.05 Enter just a real number rounded off to two decimal places.
(Short Answer)
4.9/5  (30)
(30)
Which of the graphs below could not possibly be the graph of a probability function f(x)? 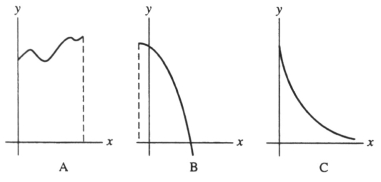
(Multiple Choice)
4.9/5  (35)
(35)
Let X be a continuous random variable A ? X ? B and let f (x) be its probability density function and F (x) its cumulative distribution function. Indicate whether the following statements are true or false.
-
(True/False)
4.9/5  (24)
(24)
Given the density function f(x) = , 0 ≤ x ≤ 4, determine the corresponding cumulative distribution function.
Enter just an unlabeled polynomial in x in standard form.
(Short Answer)
4.9/5  (31)
(31)
A survey shows that the time spent in a checkout line in a certain supermarket has an exponential density function with mean 5 minutes. What is the probability of spending 10 minutes or more in a checkout line? Enter just a real number rounded off to two decimal places.
(Short Answer)
4.9/5  (22)
(22)
Find (by inspection) the expected value and standard deviation of the random variable with the following density function: Enter your answer as just two numbers (a real number to one decimal place followed by a reduced fraction) separated by a comma, the first representing E(X) and the second representing .
(Short Answer)
4.9/5  (36)
(36)
Let X be a continuous random variable A ≤ X ≤ B and let f (x) be its probability density function and F (x) its cumulative distribution function. Indicate whether the following statements are true or false.
-Pr(a ≤ X ≤ b) =
(True/False)
4.8/5  (35)
(35)
A farmer has observed that the time to maturation of a certain crop is approximately normally distributed with a mean of 60 days and a standard deviation of 2 days. Find the percentage of plants that will mature in less than 55 days. Enter the percentage as just a real number rounded off to two decimal places followed by %.
(Short Answer)
4.8/5  (36)
(36)
A set of exam scores is 80, 75, 85, 90, 100, 70, 60. The standard deviation equals
(Multiple Choice)
4.8/5  (30)
(30)
Find the value of k that makes f(x) = a probability density function on the interval .
Enter just an integer.
(Short Answer)
5.0/5  (29)
(29)
Find the value of k that makes f(x) = a probability density function on the interval Enter just an integer.
(Short Answer)
4.9/5  (33)
(33)
Find the expected value and variance for the random variable whose probability density function is Enter just two reduced fractions (unlabeled) in the order E(X), Var(X) separated by a comma.
(Short Answer)
4.8/5  (37)
(37)
The probability density function of a continuous random variable X is , . Is this the graph of f(x) with the shaded area corresponding to ? 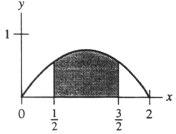
(True/False)
4.7/5  (33)
(33)
Suppose f(x) = is a probability density function for x ≥ 1. Find Pr(2 ≤ X ≤ 10).
Enter just a reduced fraction.
(Short Answer)
4.9/5  (32)
(32)
John would like to place a two dollar bet on his favorite racehorse, Black Velvet. He can bet that Black Velvet will win or show (finish in the top three horses). If he bets correctly that Black Velvet wins, he wins $20. If he bets correctly that Black Velvet shows, he wins $7. John figures Black Velvet has a 20% chance of winning and a 70% chance of showing. If X is the amount of money John wins if he bets Black Velvet will win and Y is the amount of money he wins if Black Velvet will show, find E(X) and E(Y) . Enter just two real numbers rounded off to two decimal places in the order given above representing dollars (no units).
(Short Answer)
4.8/5  (28)
(28)
A table saw cuts construction studding. Observation has shown that the lengths of the studs are normally distributed with a mean of 10 feet and a standard deviation of 6 inches. Which of the following correctly represents the probability that a randomly chosen stud exceeds 11 feet?
(Multiple Choice)
4.9/5  (39)
(39)
The table below is the probability table for a random variable X. Find Var(X). Outcome -3 -2 -1 1 2 3 Probability 0.1 0.1 0.4 0.3 0.05 0.05 Enter just a real number rounded off to two decimal places.
(Short Answer)
4.7/5  (32)
(32)
A random variable X has a density function f(x) = , 3 ≤ x ≤ 6. Find b such that .
Enter your answer exactly in the reduced form a , unlabeled.
(Short Answer)
4.8/5  (33)
(33)
A basketball player attempts successive free throws until he succeeds in making a basket. Suppose the probability of success of each attempt is 0.7; thus, the probability of exactly n failures before the first success is (0.7), n ≥ 0. What is the probability that the number of failures before the first successful free throw is odd? Enter just a reduced fraction.
(Short Answer)
4.8/5  (38)
(38)
The riders of the New Town Elementary school bus consists of 5 five year olds, 3 six year olds, 10 eight year olds, 1 nine year old, 4 eleven year olds and a twelve year old. A child is selected at random and her age is noted. Let X be the outcome. Find E(X). Enter just a reduced fraction of form (no label).
(Short Answer)
4.8/5  (34)
(34)
Showing 21 - 40 of 92
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)