Exam 10: Introducing Probability

A geneticist developed a new type of pest-resistant walnut tree. These walnut trees produce 75% of pest-resistant walnut trees and 25% of susceptible (not resistant) trees when two resistant trees are crossed. If two such trees are crossed, we will get:

An urn contains 2 red and 2 green marbles. We pick a marble, record its color, and replace it. We repeat this procedure a second and a third time. The probability distribution for the number of red marbles is given below. For this distribution, the probability of exactly one red marble is given by:

An urn contains 3 red, 2 blue, and 5 green marbles. If we pick 4 marbles with replacement and count the number of red marbles in the 4 picks, the random variable is:

I choose a card at random from a well-shuffled deck of 52 cards. There is a 1/4 probability that the card chosen is a spade, a 1/4 probability that the card is a heart, a 1/4 probability that the card is a diamond, and a 1/4 probability that the card is a club. Both spades and clubs are black cards, whereas hearts and diamonds are red. The probability that the card chosen is not a spade is:

You toss a thumbtack 100 times and observe that it lands point down 65 times. The proportion of times it landed point down is then 0.65. This proportion represents:

A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 40% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest, for the rest, susceptibility status is undetermined. The probability of knowing that a tree from a crossing is at least somewhat resistant is:

According to the M&Ms Web site, each package of the milk chocolate candies typically contains 14% brown, 13% red, 14% yellow, 16% green, 24% blue, and 20% orange M&Ms. You go to the store and buy a standard package. When you open it, you find that it contains 51 M&Ms, distributed as follows. 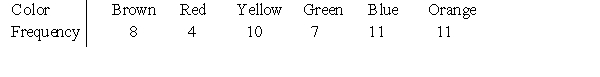The variable color is:

At a small college, all entering freshmen must take a foreign language class, chosen from the languages Spanish, French, Swahili, Chinese, and Arabic. Because there is limited space in the foreign language courses, a student cannot simultaneously enroll in more than one course. The probability distribution for the language studied by a randomly selected freshman is summarized in the following table. The probability that the freshman is studying Spanish is:

A geneticist is conducting research on pest-resistant walnut trees. He has developed a set of trees, when crossed, to produce offspring as follows: 40% of all trees are very resistant, 30% of trees are somewhat resistant, and 20% are susceptible to invasion by pest, for the rest, susceptibility status is undetermined. The probability of a tree from a crossing being not resistant or an unknown status is:

Every year, the veterinary hospital at a major research university treats a number of horses that have stones called enteroliths in their guts. A sample of 20 years shows that on average about 2% of horses presenting at the veterinary hospital are treated for enteroliths. Some breeds of horses seem more prone to developing enteroliths than others. Below is a table with the distribution of enteroliths among the breeds. 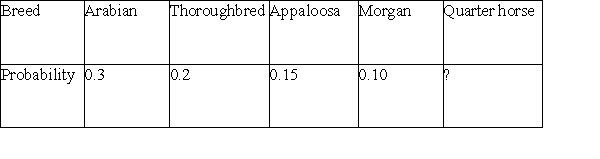The probability that a horse arriving at the veterinary hospital is not an Arabian or a quarter horse is:

The probability density of a random variable X is given in the following figure. 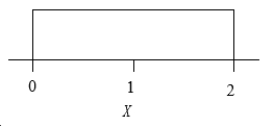From this density, the probability that X is between 0.5 and 1.5 is:

A sample of horses admitted to a local veterinary hospital had the following distribution of mares, geldings, and stallions. If we assume that the horses constitute a random sample of all horses in the state, then we estimate the probability that a randomly selected horse is a stallion to be:

An urn contains 2 red and 2 green marbles. We pick a marble, record its color, and replace it. We repeat this procedure a second and a third time. The probability distribution for the number of red marbles is given by:

A random variable can be described as:

Horses are housed in pastures, pipe pens, or barn stalls at a local horse barn. Let X = the number of horses housed in barn stalls. Then X is:

A randomly selected sample of 100 horse owners found that 72 of them feed grass hay to their horses in the morning and alfalfa in the evening. The value 0.72 represents:

A geneticist developed a new type of pest-resistant walnuts. These walnuts produce 75% of pest-resistant walnut trees and 25% of susceptible (not resistant) trees when two resistant trees are crossed. If a grower crossed 100 such pairs of trees for 100 offspring and did this many times over many years and plots, she should get:

A North American roulette wheel has 38 slots, of which 18 are red, 18 are black, and 2 are green. If you bet on red, the probability of winning is 18/38 = 0.4737. The probability 0.4737 represents:

A randomly selected sample of 100 horse owners found that 72 of them feed one flake of alfalfa plus one flake of grass hay in the evening to their horses, while the rest feed one flake of alfalfa plus oat hay in the evening. The estimated probability that horse owners feed alfalfa plus oat hay in the evening is:

Suppose we roll two fair four-sided dice. Let X denote the sum of the two roll outcomes. For example, if the first roll yields 3 and the second roll yields 1, then X = 3 + 1 = 4. The probability distribution for X is given below. 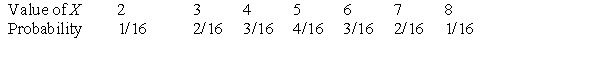The probability of rolling a pair of 4s is: