Exam 4: Analyzing Change: Applications of Derivatives
Exam 1: Ingredients of Change: Functions an Limits50 Questions
Exam 2: Describing Change: Rates47 Questions
Exam 3: Determining Change: Derivatives48 Questions
Exam 4: Analyzing Change: Applications of Derivatives50 Questions
Exam 5: Accumulating Change: Limits of Sums and the Definite Integral50 Questions
Exam 6: Analyzing Accumulated Change: Integrals in Action51 Questions
Exam 7: Ingredients of Multivariable Change: Models, Graphs, Rates46 Questions
Exam 8: Analyzing Multivariable Change: Optimization50 Questions
Select questions type
Estimate the input value(s) where the function has a relative extreme point. Identify each relative extreme as a maximum or minimum, and indicate whether the derivative of the function at that point is zero or does not exist. 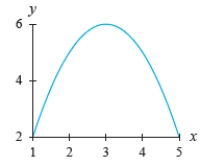
(Multiple Choice)
4.8/5  (30)
(30)
The amount in an investment after t years is given by 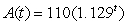 thousand dollars Find the rate of change for the amount after 13 years and interpret the answer.
thousand dollars Find the rate of change for the amount after 13 years and interpret the answer.
(Multiple Choice)
4.7/5  (28)
(28)
The yearly amount of garbage (in million tons) taken to a landfill outside a city during selected years from 1980 through 2010 is given below. Write a model for the data. 
(Multiple Choice)
4.8/5  (31)
(31)
The percentage of southern Australian grasshopper eggs that hatch as a function of temperature (for temperatures between 7°C and 25°C) can be modeled as 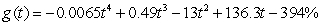 where t is the temperature in °C, data from
where t is the temperature in °C, data from 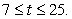 What temperature between 7°C and 25°C corresponds to the greatest percentage of eggs hatching? What is the percentage at this input?
What temperature between 7°C and 25°C corresponds to the greatest percentage of eggs hatching? What is the percentage at this input?
(Multiple Choice)
4.8/5  (48)
(48)
Calculate the derivative of the function with the appropriate formula. 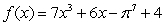
(Multiple Choice)
4.9/5  (33)
(33)
Suppose the revenue from new car sales between 1980 and 2000 can be modeled as a function of advertising expenditures, by 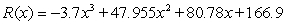 billion dollars of revenue, when x billion dollars is spent on advertising, for
billion dollars of revenue, when x billion dollars is spent on advertising, for 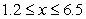 . What does the model estimate as the revenue when $5.8 billion is spent on advertising? Round your answer to the nearest billion dollars.
. What does the model estimate as the revenue when $5.8 billion is spent on advertising? Round your answer to the nearest billion dollars.
(Multiple Choice)
4.7/5  (30)
(30)
A pizza parlor has been experimenting with lowering the price of their large one-topping pizza to promote sales. The average revenues from the sale of large one-topping pizzas on a Friday night (5 P.M. to midnight) at various prices are given below. Find a model for the data. 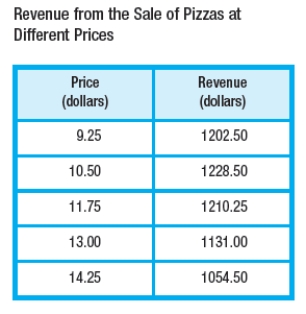
(Multiple Choice)
4.9/5  (34)
(34)
A function and its first and second derivatives are given. Use these to find any points of inflection. 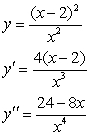
(Multiple Choice)
4.9/5  (26)
(26)
A function and its first and second derivatives are given. Use these to find all critical values. 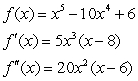
(Multiple Choice)
4.7/5  (38)
(38)
A softball diamond is a square with each side measuring 60 feet. Suppose a player is running from second base to third base at a rate of 22 feet per second. At what rate is the distance between the runner and home plate changing when the runner is halfway to third base?
(Multiple Choice)
4.9/5  (36)
(36)
For fiddler crabs, the weight of the claw can be modeled as 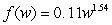 pounds when the weight of the body is w pounds. Describe the direction and concavity of
pounds when the weight of the body is w pounds. Describe the direction and concavity of 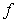 for positive values of w.
for positive values of w.
(Multiple Choice)
4.8/5  (48)
(48)
The figure shows the annual cost for a one-million-dollar term life insurance policy as a function of the age of the insured person. 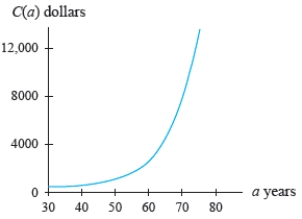 Write the linearization of C at 60.
Write the linearization of C at 60.
(Multiple Choice)
4.8/5  (34)
(34)
A portion of the shoreline of an island is in the shape of the curve 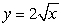 . A hut is located at point C, as shown below. Supplies are delivered by boat to the shoreline. It costs $10 per mile to hire someone to transport the supplies from the shore to the hut. How much does the overland transportation cost?
. A hut is located at point C, as shown below. Supplies are delivered by boat to the shoreline. It costs $10 per mile to hire someone to transport the supplies from the shore to the hut. How much does the overland transportation cost? 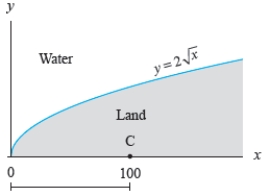
(Multiple Choice)
4.8/5  (34)
(34)
Showing 21 - 40 of 50
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)