Exam 4: Applications of the Derivative
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
Use the information summarized in the table to select the graph of f. 
(Multiple Choice)
4.9/5  (25)
(25)
A stone is thrown straight up from the roof of an 60-ft building. The height (in feet) of the stone at any time t (in seconds), measured from the ground, is given by 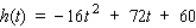 .
What is the maximum height the stone reaches?
__________ ft
.
What is the maximum height the stone reaches?
__________ ft
(Short Answer)
4.8/5  (36)
(36)
In the diagram, S represents the position of a power relay station located on a straight coast, and E shows the location of a marine biology experimental station on an island. A cable is to be laid connecting the relay station with the experimental station. 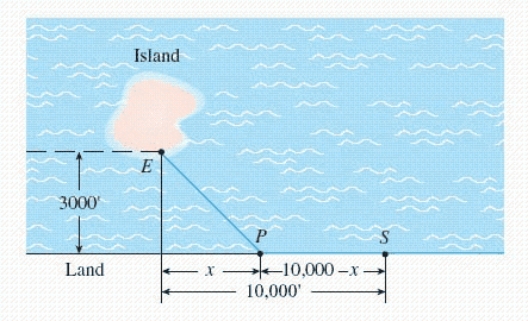 If the cost of running the cable on land is $3.60/running foot and the cost of running the cable under water is $6.00/running foot, locate the point P that will result in a minimum cost (solve for x).
If the cost of running the cable on land is $3.60/running foot and the cost of running the cable under water is $6.00/running foot, locate the point P that will result in a minimum cost (solve for x). 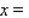 __________ ft
__________ ft
(Short Answer)
4.8/5  (37)
(37)
The demand for motorcycle tires imported by Dixie Import-Export is 30,000/year and may be assumed to be uniform throughout the year. The cost of ordering a shipment of tires is $300, and the cost of storing each tire for a year is $2.
Determine how many tires should be in each shipment if the ordering and storage costs are to be minimized. (Assume that each shipment arrives just as the previous one has been sold.)
__________ tires
(Short Answer)
5.0/5  (33)
(33)
For its beef stew, Betty Moore Company uses aluminum containers that have the form of right circular cylinders. Find the radius and height of a container if it has a capacity of 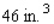 and is constructed using the least amount of metal.
and is constructed using the least amount of metal.
(Multiple Choice)
4.7/5  (39)
(39)
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 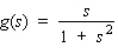
(Multiple Choice)
4.7/5  (39)
(39)
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 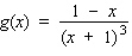
(Multiple Choice)
4.8/5  (43)
(43)
The quantity demanded each month of the Walter Serkin recording of Beethoven's Moonlight Sonata, manufactured by Phonola Record Industries, is related to the price/compact disc. The equation 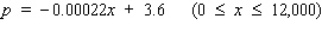 , where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by
, where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by 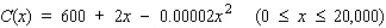 .
To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is
.
To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is 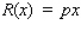 , and the profit is
, and the profit is 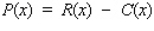 .
.
(Multiple Choice)
4.7/5  (45)
(45)
Find the interval(s) where the function is increasing and the interval(s) where it is decreasing. 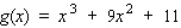
(Multiple Choice)
4.7/5  (34)
(34)
A rectangular box is to have a square base and a volume of 4 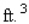 . If the material for the base costs 20 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 10 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost.
. If the material for the base costs 20 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 10 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost. 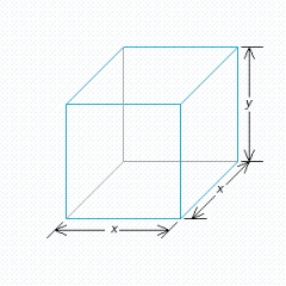
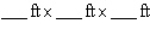
(Essay)
4.8/5  (28)
(28)
The level of ozone, an invisible gas that irritates and impairs breathing, present in the atmosphere on a certain May day in the city was approximated by 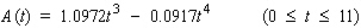 , where
, where 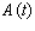 is measured in pollutant standard index (PSI) and
is measured in pollutant standard index (PSI) and 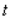 is measured in hours, with
is measured in hours, with 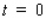 corresponding to
corresponding to 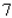 a.m.
Use the second derivative test to show that the function
a.m.
Use the second derivative test to show that the function 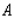 has a relative maximum at approximately
has a relative maximum at approximately 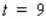 . Interpret your results.
. Interpret your results.
(Essay)
4.9/5  (38)
(38)
The estimated monthly profit (in dollars) realizable by Cannon Precision Instruments for manufacturing and selling x units of its model M1 camera is 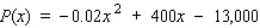 To maximize its profits, how many cameras should Cannon produce each month?
To maximize its profits, how many cameras should Cannon produce each month?
(Multiple Choice)
4.8/5  (38)
(38)
Find the horizontal and vertical asymptotes of the graph of the function. 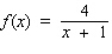
(Multiple Choice)
4.9/5  (39)
(39)
Find the relative maxima and relative minima, if any, of the function. Otherwise, answer none. 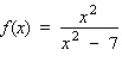 Relative maxima: __________
Relative minima: __________
Relative maxima: __________
Relative minima: __________
(Essay)
4.8/5  (40)
(40)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false. If f is increasing on (a, b), then 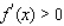 for each x in (a, b).
for each x in (a, b).
(Multiple Choice)
4.8/5  (31)
(31)
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 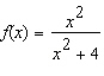
(Multiple Choice)
4.8/5  (42)
(42)
By cutting away identical squares from each corner of a rectangular piece of cardboard and folding up the resulting flaps, an open box may be made. If the cardboard is 8 in. long and 3 in. wide, find the dimensions of the box that will yield the maximum volume. 
(Essay)
5.0/5  (36)
(36)
One of the functions below is the derivative function of the other. Identify each of them. 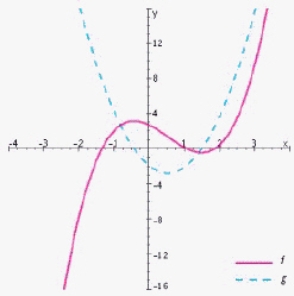
(Essay)
4.9/5  (35)
(35)
Using the curve-sketching guide, select the graph of the function. 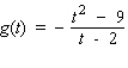
(Multiple Choice)
4.8/5  (34)
(34)
Showing 41 - 60 of 182
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)