Exam 4: Applications of the Derivative
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
The figure depicts a racetrack with ends that are semicircular in shape. The length of the track is 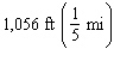 .
.  Find
Find 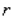 and
and 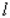 so that the area enclosed by the rectangular region of the racetrack is as large as possible.
so that the area enclosed by the rectangular region of the racetrack is as large as possible.
(Multiple Choice)
4.8/5  (36)
(36)
A wooden beam has a rectangular cross section of height 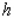 in. and width
in. and width 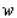 in. (see the figure). The strength
in. (see the figure). The strength 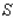 of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross section of the strongest beam that can be cut from a round log of diameter 24 in.? Hint:
of the beam is directly proportional to its width and the square of its height. What are the dimensions of the cross section of the strongest beam that can be cut from a round log of diameter 24 in.? Hint: 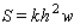 , where
, where 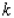 is a constant of proportionality.
is a constant of proportionality. 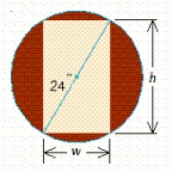
(Multiple Choice)
4.8/5  (41)
(41)
A manufacturer of tennis rackets finds that the total cost C(x) (in dollars) of manufacturing x rackets/day is given by 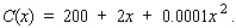 Each racket can be sold at a price of p dollars, where p is related to x by the demand equation
Each racket can be sold at a price of p dollars, where p is related to x by the demand equation 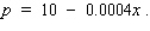 If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
(Multiple Choice)
4.9/5  (36)
(36)
An apple orchard has an average yield of 48 bushels of apples/tree if tree density is 24 trees/acre. For each unit increase in tree density, the yield decreases by 3 bushels. How many trees should be planted in order to maximize the yield?
__________ trees
(Short Answer)
4.9/5  (39)
(39)
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 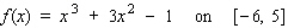
(Multiple Choice)
4.7/5  (38)
(38)
The average cost per disc (in dollars) incurred by Herald Records in pressing x DVDs is given by the average cost function 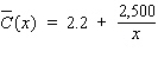 Find the horizontal asymptote of
Find the horizontal asymptote of 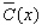 .
__________
What is the limiting value of the average cost?
__________
.
__________
What is the limiting value of the average cost?
__________
(Essay)
4.8/5  (40)
(40)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
If f is decreasing on (a, b), then 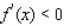 for each x in (a, b).
for each x in (a, b).
(True/False)
4.8/5  (30)
(30)
Postal regulations specify that a parcel sent by parcel post may have a combined length and girth of no more than 102 in. Find the dimensions of a rectangular package that has a square cross section and the largest volume that may be sent through the mail. What is the volume of such a package? (Hint: The length plus the girth is 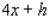 (see the figure)).
(see the figure)). 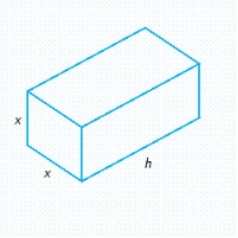
(Multiple Choice)
4.8/5  (30)
(30)
Find the absolute maximum value and the absolute minimum value, if any, of the given function. 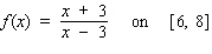
(Multiple Choice)
4.8/5  (47)
(47)
Using the curve-sketching guide, select the graph of the function. 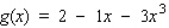
(Multiple Choice)
4.8/5  (36)
(36)
The total annual revenue 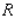 of the Miramar Resorts Hotel is related to the amount of money
of the Miramar Resorts Hotel is related to the amount of money 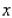 the hotel spends on advertising its services by the function
the hotel spends on advertising its services by the function 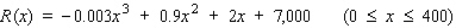 where both
where both 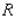 and
and 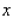 are measured in thousands of dollars. Use this function to:
A. Find the interval where the graph of
are measured in thousands of dollars. Use this function to:
A. Find the interval where the graph of 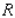 is concave upward and the interval where the graph of
is concave upward and the interval where the graph of 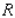 is concave downward.
B. Find the inflection point of
is concave downward.
B. Find the inflection point of 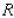 .
C. Determine if it would it be more beneficial for the hotel to increase its advertising budget slightly when the budget is $90,000 or when it is $110,000.
.
C. Determine if it would it be more beneficial for the hotel to increase its advertising budget slightly when the budget is $90,000 or when it is $110,000.
(Multiple Choice)
4.8/5  (41)
(41)
Find the relative extrema of the following function. Use the second derivative test, if applicable. 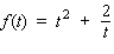
(Multiple Choice)
4.8/5  (35)
(35)
A stone is thrown straight up from the roof of a 50-ft building. The height (in feet) of the stone at any time t (in seconds), measured from the ground, is given by 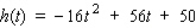 What is the maximum height the stone reaches?
What is the maximum height the stone reaches?
(Multiple Choice)
4.9/5  (38)
(38)
A division of Chapman Corporation manufactures a pager. The weekly fixed cost for the division is $20,000, and the variable cost for producing x pagers/week is 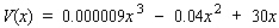 dollars. The company realizes a revenue of
dollars. The company realizes a revenue of 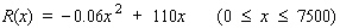 dollars from the sale of x pagers/week.
Find the level of production that will yield a maximum profit for the manufacturer. (Hint: Use the quadratic formula.)
__________ pagers/week
dollars from the sale of x pagers/week.
Find the level of production that will yield a maximum profit for the manufacturer. (Hint: Use the quadratic formula.)
__________ pagers/week
(Short Answer)
4.9/5  (28)
(28)
Use the information summarized in the table to select the graph of f. 
(Multiple Choice)
4.7/5  (34)
(34)
Find the interval(s) where the function is increasing and the interval(s) where it is decreasing. 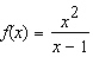
(Multiple Choice)
4.9/5  (36)
(36)
Select the graph of the function using the curve-sketching guide. 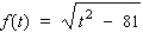
(Multiple Choice)
4.9/5  (37)
(37)
The number of major crimes committed in the city between 1997 and 2004 is approximated by the function 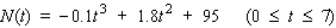 where N(t) denotes the number of crimes committed in year t (
where N(t) denotes the number of crimes committed in year t ( 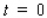 corresponds to 1997). Enraged by the dramatic increase in the crime rate, the citizens, with the help of the local police, organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace.
Show that the growth in the crime rate was maximal in 2003, giving credence to the claim that the Neighborhood Crime Watch program was working.
corresponds to 1997). Enraged by the dramatic increase in the crime rate, the citizens, with the help of the local police, organized "Neighborhood Crime Watch" groups in early 2001 to combat this menace.
Show that the growth in the crime rate was maximal in 2003, giving credence to the claim that the Neighborhood Crime Watch program was working.
(Essay)
4.9/5  (39)
(39)
Showing 81 - 100 of 182
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)