Exam 4: Applications of the Derivative
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
If exactly 150 people sign up for a charter flight, Leisure World Travel Agency charges $250/person. However, if more than 150 people sign up for the flight (assume this is the case), then each fare is reduced by $1 for each additional person. Determine how many passengers will result in a maximum revenue for the travel agency. What is the maximum revenue? What would be the fare per passenger in this case?
Hint: Let x denote the number of passengers above 150. Show that the revenue function R is given by R(x) = (150 + x)(250 - x).
(Multiple Choice)
4.7/5  (34)
(34)
A stone is thrown straight up from the roof of an 48-ft building. The distance (in feet) of the stone from the ground at any time t (in seconds) is given by 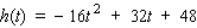 . Sketch the graph of h. When is the stone rising, and when is it falling? If the stone were to miss the building, when would it hit the ground?
. Sketch the graph of h. When is the stone rising, and when is it falling? If the stone were to miss the building, when would it hit the ground?
(Multiple Choice)
4.7/5  (29)
(29)
The quantity demanded each month of the Sicard wristwatch is related to the unit price by the equation 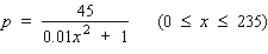 , where p is measured in dollars and x is measured in units of a thousand.
To yield a maximum revenue, how many watches must be sold?
, where p is measured in dollars and x is measured in units of a thousand.
To yield a maximum revenue, how many watches must be sold? 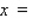 __________
__________
(Short Answer)
4.8/5  (37)
(37)
What are the dimensions of a closed rectangular box that has a square cross section, a capacity of 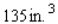 and is constructed using the least amount of material?
and is constructed using the least amount of material?
(Multiple Choice)
4.8/5  (33)
(33)
Find the horizontal and vertical asymptotes of the graph. 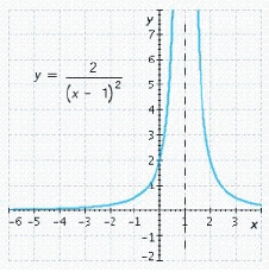 Horizontal asymptote is __________
Vertical asymptote is __________
Horizontal asymptote is __________
Vertical asymptote is __________
(Essay)
4.8/5  (39)
(39)
The level of ozone, an invisible gas that irritates and impairs breathing, present in the atmosphere on a certain May day in the city was approximated by 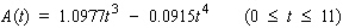 where
where  is measured in pollutant standard index (PSI) and
is measured in pollutant standard index (PSI) and  is measured in hours, with
is measured in hours, with 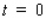 corresponding to
corresponding to 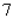 a.m. Use the second derivative test to find the approximate value of
a.m. Use the second derivative test to find the approximate value of 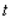 where the function
where the function 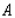 has a relative maximum. Round to the nearest integer.
has a relative maximum. Round to the nearest integer.
(Multiple Choice)
4.9/5  (31)
(31)
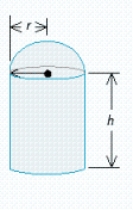
A grain silo has the shape of a right circular cylinder surmounted by a hemisphere (see the figure). If the silo is to have a capacity of 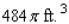 , find the radius and height of the silo that requires the least amount of material to construct. Hint: The volume of the silo is
, find the radius and height of the silo that requires the least amount of material to construct. Hint: The volume of the silo is 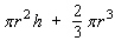 , and the surface area (including the floor) is
, and the surface area (including the floor) is 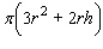 .
. 
(Multiple Choice)
4.9/5  (34)
(34)
Find the relative maxima and relative minima, if any, of the function. Otherwise, answer none. 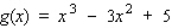 Relative minima: __________
Relative maxima: __________
Relative minima: __________
Relative maxima: __________
(Essay)
4.9/5  (38)
(38)
If f is not continuous on the closed interval 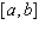 , then f cannot have an absolute maximum value.
, then f cannot have an absolute maximum value.
(Multiple Choice)
4.8/5  (32)
(32)
Neilsen Cookie Company sells its assorted butter cookies in containers that have a net content of 1 lb. The estimated demand for the cookies is 1,000,000 1-lb containers. The setup cost for each production run is $250, and the manufacturing cost is $.50 for each container of cookies. The cost of storing each container of cookies over the year is $.20.
Assuming uniformity of demand throughout the year and instantaneous production, how many containers of cookies should Neilsen produce per production run in order to minimize the production cost?
Hint: Show that the total production cost is given by the function 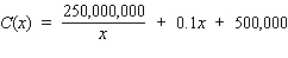 .
Then minimize the function
.
Then minimize the function 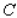 on the interval (0, 1,000,000).
__________ containers of cookies per production run
on the interval (0, 1,000,000).
__________ containers of cookies per production run
(Short Answer)
4.9/5  (30)
(30)
A manufacturer of tennis rackets finds that the total cost C(x) (in dollars) of manufacturing x rackets/day is given by 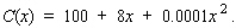 Each racket can be sold at a price of p dollars, where p is related to x by the demand equation
Each racket can be sold at a price of p dollars, where p is related to x by the demand equation 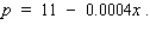 If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
__________ rackets/day
If all rackets that are manufactured can be sold, find the daily level of production that will yield a maximum profit for the manufacturer.
__________ rackets/day
(Short Answer)
4.9/5  (35)
(35)
Find the horizontal and vertical asymptotes of the graph of the function. 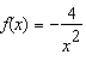
(Multiple Choice)
4.7/5  (32)
(32)
The quantity demanded each month of the Sicard wristwatch is related to the unit price by the equation 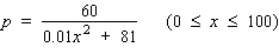 , where p is measured in dollars and x is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?
, where p is measured in dollars and x is measured in units of a thousand. To yield a maximum revenue, how many watches must be sold?
(Multiple Choice)
4.8/5  (38)
(38)
A book designer has decided that the pages of a book should have 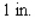 margins at the top and bottom and
margins at the top and bottom and 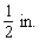 margins on the sides. She further stipulated that each page should have an area of
margins on the sides. She further stipulated that each page should have an area of 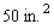 (see the figure).
(see the figure). 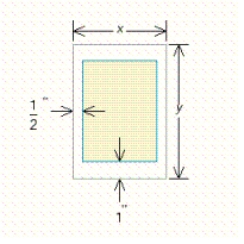 Determine the page dimensions that will result in the maximum printed area on the page.
Determine the page dimensions that will result in the maximum printed area on the page.
(Multiple Choice)
4.7/5  (45)
(45)
You are given the graph of a function f. Determine the intervals where f is increasing, constant, or decreasing. 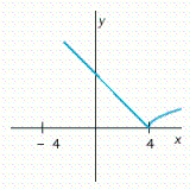
(Multiple Choice)
4.8/5  (41)
(41)
You are given the graph of some function f defined on the indicated interval. Find the absolute maximum and the absolute minimum of f, if they exist. 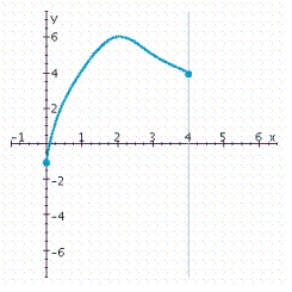
(Multiple Choice)
4.9/5  (31)
(31)
The quantity demanded each month of the Walter Serkin recording of Beethoven's Moonlight Sonata, manufactured by Phonola Record Industries, is related to the price/compact disc. The equation 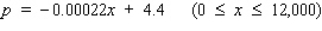 , where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by
, where p denotes the unit price in dollars and x is the number of discs demanded, relates the demand to the price.
The total monthly cost (in dollars) for pressing and packaging x copies of this classical recording is given by 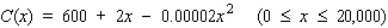 .
To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is
.
To maximize its profits, how many copies should Phonola produce each month? Hint: The revenue is 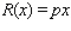 , and the profit is
, and the profit is 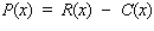 .
. 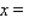 __________ copies
__________ copies
(Short Answer)
4.7/5  (43)
(43)
Showing 121 - 140 of 182
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)