Exam 4: Applications of the Derivative
Exam 1: Preliminaries205 Questions
Exam 2: Functions, Limits and the Derivative269 Questions
Exam 3: Differentiation330 Questions
Exam 4: Applications of the Derivative182 Questions
Exam 5: Exponential and Logarithmic Functions278 Questions
Exam 6: Integration314 Questions
Exam 7: Additional Topics in Integration250 Questions
Exam 8: Calculus of Several Variables206 Questions
Select questions type
Find the interval(s) where the function is increasing and the interval(s) where it is decreasing. f (x) = -6x + 4
(Multiple Choice)
4.9/5  (31)
(31)
Select the graph of the function using the curve-sketching guide. 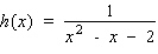
(Multiple Choice)
4.8/5  (41)
(41)
Find the horizontal and vertical asymptotes of the graph of the function. 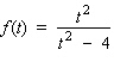
(Multiple Choice)
4.9/5  (40)
(40)
Suppose the quantity demanded per week of a certain dress is related to the unit price p by the demand equation 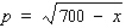 , where p is in dollars and x is the number of dresses made.
To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px.) Round the answer to the nearest integer.
__________ dresses
, where p is in dollars and x is the number of dresses made.
To maximize the revenue, how many dresses should be made and sold each week? (Hint: R(x) = px.) Round the answer to the nearest integer.
__________ dresses
(Short Answer)
4.8/5  (47)
(47)
Find the relative maxima and relative minima, if any, of the function. Otherwise, answer none. 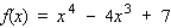 Relative minima: __________
Relative maxima: __________
Relative minima: __________
Relative maxima: __________
(Essay)
4.9/5  (30)
(30)
The average speed of a vehicle on a stretch of Route 134 between 6 a.m. and 11 a.m. on a typical weekday is approximated by the function 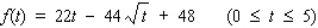 where f(t) is measured in miles per hour and t is measured in hours, with
where f(t) is measured in miles per hour and t is measured in hours, with 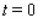 corresponding to 6 a.m. Find the interval where f is decreasing and the interval where f is increasing.
corresponding to 6 a.m. Find the interval where f is decreasing and the interval where f is increasing.
(Multiple Choice)
4.7/5  (43)
(43)
A truck gets 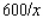 mpg when driven at a constant speed of x mph (between 50 and 70 mph). If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 50 and 70 mph is it most economical to drive?
__________ mph
mpg when driven at a constant speed of x mph (between 50 and 70 mph). If the price of fuel is $1/gallon and the driver is paid $8/hour, at what speed between 50 and 70 mph is it most economical to drive?
__________ mph
(Short Answer)
4.8/5  (39)
(39)
Find the horizontal and vertical asymptotes of the graph of the function. 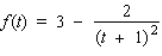
(Multiple Choice)
4.8/5  (25)
(25)
If the graph of f is concave upward on (a, b), then the graph of - f is concave upward on (a, b).
(Multiple Choice)
4.7/5  (39)
(39)
The owner of a luxury motor yacht that sails among the 4,000 Greek islands charges $600/person/day if exactly 20 people sign up for the cruise. However,if more than 20 people sign up (up to the maximum capacity of 90) for the cruise, then each fare is reduced by $4 for each additional passenger. Assuming at least 20 people sign up for the cruise, determine how many passengers will result in the maximum revenue for the owner of the yacht. What is the maximum revenue? What would be the fare/passenger in this case?
(Multiple Choice)
4.9/5  (31)
(31)
A rectangular box is to have a square base and a volume of 32 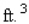 . If the material for the base costs 10 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 20 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost.
. If the material for the base costs 10 cent/square foot, the material for the sides costs 30 cent/square foot, and the material for the top costs 20 cent/square foot, determine the dimensions of the box that can be constructed at minimum cost. 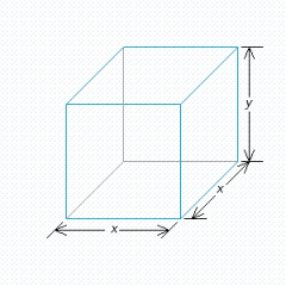
(Multiple Choice)
4.8/5  (38)
(38)
An apple orchard has an average yield of 48 bushels of apples/tree if tree density is 26 trees/acre. For each unit increase in tree density, the yield decreases by 3 bushels. How many trees should be planted in order to maximize the yield?
(Multiple Choice)
4.9/5  (42)
(42)
What are the dimensions of a closed rectangular box that has a square cross section, a capacity of 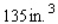 and is constructed using the least amount of material? Round the answer to two decimal places.
and is constructed using the least amount of material? Round the answer to two decimal places. 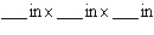
(Essay)
4.9/5  (43)
(43)
Find the interval(s) where the function is increasing and the interval(s) where it is decreasing. 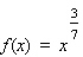
(Multiple Choice)
4.9/5  (34)
(34)
Find the absolute maximum value and the absolute minimum value, if any, of the given function. ![Find the absolute maximum value and the absolute minimum value, if any, of the given function. on [1, 5]](https://storage.examlex.com/TB6026/11eaa8b1_db59_bab4_b1b6_9587d399b114_TB6026_11.jpg) on [1, 5]
on [1, 5]
(Multiple Choice)
4.8/5  (42)
(42)
Phillip, the proprietor of a vineyard, estimates that the first 10,000 bottles of wine produced this season will fetch a profit of $2/bottle. However, the profit from each bottle beyond 10,000 drops by $0.0004 for each additional bottle sold. Assuming at least 10,000 bottles of wine are produced and sold, what is the maximum profit? What would be the price/bottle in this case?
(Multiple Choice)
4.8/5  (27)
(27)
Find the relative extrema, if any, of the function. Use the second derivative test, if applicable. 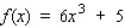
(Multiple Choice)
4.8/5  (27)
(27)
Showing 61 - 80 of 182
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)