Exam 8: Estimation and Confidence Intervals

The Sugar Producers Association wants to estimate the mean yearly sugar consumption. A sample of 16 people reveals the mean yearly consumption to be 27 kg with a sample standard deviation of 9 kg. Assume a normal population. Develop a 95% confidence interval for the mean annual consumption of sugar.

A confidence interval for a population mean

A survey of 25 grocery stores revealed that the average price of a 4-litre bag of milk was $2.98 with a standard error of $0.10. If 90% and 95% confidence intervals were developed to estimate the true cost of a 4-litre bag of milk, what similarities would they have?

The Dean of the Business School wants to estimate the mean number of hours worked per week by students. A sample of only 12 students showed a mean of 24 hours with a standard deviation of 4 hours. Find the 95 percent confidence interval for the population mean.

Dottie Kleman is the "Cookie Lady." She bakes and sells cookies at 50 different locations. Ms. Kleman is concerned about absenteeism among her workers. The information below reports the number of days absent for a sample of 10 workers during the last two-week pay period. The sample mean is calculated to be 1.8 and sample standard deviation is 1.1353. Develop a 95% confidence interval for the population mean. Assume that the population distribution is normal. Is it reasonable to conclude that the typical worker does not miss any days during a pay period?

When a confidence interval for a population mean is constructed from sample data,

The z-value associated with a 96% level of confidence is:

Dottie Kleman is the "Cookie Lady." She bakes and sells cookies at 50 different locations. Ms. Kleman is concerned about absenteeism among her workers. The information below reports the number of days absent for a sample of 10 workers during the last two-week pay period. The sample mean is calculated to be 1.8 and sample standard deviation is 1.1353. Develop a 95% confidence interval for the population mean. Assume that the population distribution is normal. Is it reasonable to conclude that the typical worker misses 1 day during a pay period?

A group of statistics students decided to conduct a survey at their university to find the average (mean) amount of time students spent studying per week. Assuming a standard deviation of 6 hours, what is the required sample size if the error is to be less than ½ hour with a 95% level of confidence?

Recently, a university surveyed recent graduates of the English Department for their starting salaries. Four hundred graduates returned the survey. The average salary was $55,000. The population standard deviation is known to be $2,500. What is the 95% confidence interval for the mean salary of all graduates from the English Department?

i. The t distribution is based on the assumption that the population of interest is normal or nearly normal. ii. The t distribution is a continuous distribution. iii. There is not one t distribution, but rather a "family" of t distributions.

A survey of an urban university (population of 25,450) showed that 870 of 1,100 students sampled supported a fee increase to fund improvements to the student recreation center. Using the 95% level of confidence, what is the confidence interval?

The Sugar Producers Association wants to estimate the mean yearly sugar consumption. A sample of 16 people reveals the mean yearly consumption to be 27 kg with a sample standard deviation of 9 kg. Assume a normal population. For a 99% confidence interval, what is the critical value needed?

A sample of 50 is selected from a known population of 250 elements. The population standard deviation is 15. What is the standard error of the sample means using the finite population correction factor?

The manager of the college cafeteria wants to estimate the mean amount spent per customer per purchase. A sample of 10 customers revealed the following amounts spent: Find the 99 percent confidence limits for the mean amount spent. Sample mean = $4.53, s = $1.00

A sample of 25 is selected from a known population of 100 elements. What is the finite population correction factor?

The mean number of travel days per year for the outside salespeople employed by hardware distributors is to be estimated. The 0.90 degree of confidence is to be used. The mean of a small pilot study was 150 days, with a standard deviation of 14 days. If the population mean is to be estimated within two days, how many outside salespeople should be sampled?

A manager of a local store wants to estimate the mean amount spent per shopping visit by customers. Summary statistics from a sample taken reveal the following: 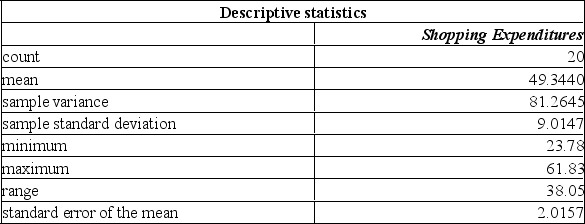If 90% and 95% confidence intervals were developed to estimate the true shopping expenditure, what similarities would exist?

The following summarizes the amount of snowfall in Ontario over the past number of years. 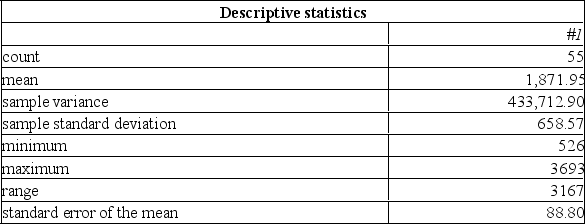If 95% and 98% confidence intervals were developed to estimate the true average annual snowfall, what differences would exist?

Dr. Patton is a professor of English. Recently she counted the number of misspelled works in a group of student essays. She noted the distribution of misspelled words per essay followed the normal distribution with a standard deviation of 2.44 words per essay. For her Tuesday class of 50 students, the mean number of misspelled words per essay was 6.05. Construct a 99% confidence interval for the mean number of misspelled words in the population of student essays.