Exam 8: Estimation and Confidence Intervals
Exam 1: What Is Statistics79 Questions
Exam 2: Describing Data: Frequency Tables, Frequency Distributions, and Graphic Presentation87 Questions
Exam 3: Describing Data: Numerical Measures191 Questions
Exam 4: A Survey of Probability Concepts130 Questions
Exam 5: Discrete Probability Distributions121 Questions
Exam 6: Continuous Probability Distributions143 Questions
Exam 7: Sampling Methods and the Central Limit Theorem78 Questions
Exam 8: Estimation and Confidence Intervals134 Questions
Exam 9: One-Sample Tests of Hypothesis139 Questions
Exam 10: Two-Sample Tests of Hypothesis103 Questions
Exam 11: Analysis of Variance97 Questions
Exam 12: Linear Regression and Correlation166 Questions
Exam 13: Multiple Regression and Correlation Analysis128 Questions
Exam 14: Chi-Square Applications126 Questions
Exam 15: Index Numbers93 Questions
Exam 16: Time Series and Forecasting90 Questions
Exam 17: An Introduction to Decision Theory54 Questions
Select questions type
A 95% confidence interval infers that the population mean is
(Multiple Choice)
4.8/5  (39)
(39)
The t distribution is similar to the z distribution in all BUT ONE of the following characteristics. Which one is it?
(Multiple Choice)
4.9/5  (34)
(34)
(i. The point estimate states the range within which a population parameter probably lies.
(ii). The measure of confidence that one has in the interval estimate is called degree of level of confidence.
(iii) For a sampling distribution of the means, 95% percent of the means would be between 1.96 standard deviations.
(Multiple Choice)
4.8/5  (39)
(39)
The Sugar Producers Association wants to estimate the mean yearly sugar consumption. A sample of 25 people reveals the mean yearly consumption to be 27 kg with a sample standard deviation of 9 kg. Assume a normal population. Develop a 99% confidence interval for the mean annual consumption of sugar.
(Multiple Choice)
4.8/5  (32)
(32)
A manager of a local store wants to estimate the mean amount spent per shopping visit by customers. Summary statistics from a sample taken reveal the following: 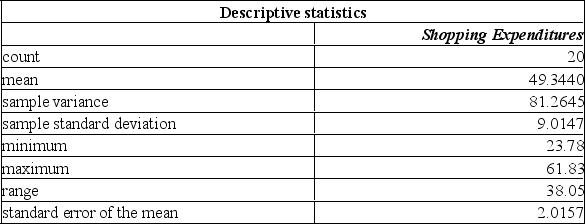 The store manager wonders whether the population mean could have been $50 or $60.
The store manager wonders whether the population mean could have been $50 or $60.
(Multiple Choice)
4.8/5  (29)
(29)
How does the t distribution differ from the standard z distribution?
(Multiple Choice)
4.9/5  (30)
(30)
A statistics professor wishes to estimate the average mark on a term test for a course that has multiple sections and many students. A survey of some of the students registered for the course reveals the following results: 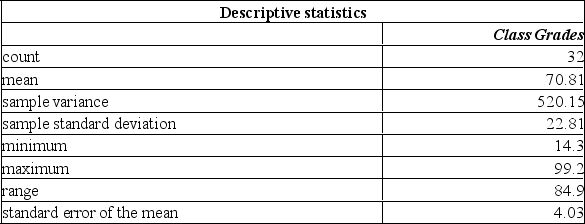 If 95% and 98% confidence intervals were developed to estimate the true term test mean, what differences would exist?
If 95% and 98% confidence intervals were developed to estimate the true term test mean, what differences would exist?
(Multiple Choice)
4.9/5  (27)
(27)
Determine the sample size that is required to estimate a population mean to within 0.4 units with a 99% confidence when the population standard deviation is 1.75.
(Multiple Choice)
4.8/5  (35)
(35)
A sample of 20 is selected from the population. What is the number of degrees of freedom used to determine the appropriate critical t-value?
(Multiple Choice)
4.9/5  (38)
(38)
Recently, a university surveyed recent graduates of the English Department for their starting salaries. Four hundred graduates returned the survey. The average salary was $55,000 with a standard deviation of $2,500. What is the best point estimate of the population mean?
(Multiple Choice)
4.8/5  (37)
(37)
Suppose 1,600 of 2,000 registered voters sampled said they planned to vote for a particular candidate. Using the 0.95 degree of confidence, what is the interval estimate for the population proportion (to the nearest tenth of a percent)?
(Multiple Choice)
4.9/5  (27)
(27)
College X is concerned about their employees making use of their email for non-business purposes. A random sample of 400 e-mails discovered 40 messages that were not business related. The 95% confidence interval for the population proportion is:
(Multiple Choice)
4.8/5  (31)
(31)
Dr. Patton is a professor of English. Recently she counted the number of misspelled works in a group of student essays. She noted the distribution of misspelled words per essay followed the normal distribution with a standard deviation of 2.44 words per essay. For her Tuesday class of 50 students, the mean number of misspelled words per essay was 6.05. Construct a 95% confidence interval for the mean number of misspelled words in the population of student essays.
(Multiple Choice)
4.9/5  (29)
(29)
A manager of a local store wants to estimate the mean amount spent per shopping visit by customers. Summary statistics from a sample taken reveal the following: 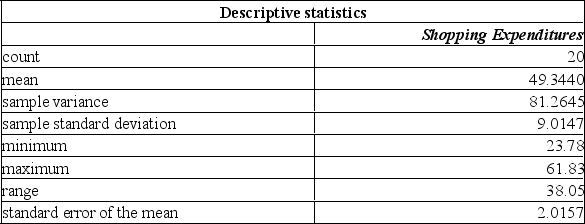 If 95% and 98% confidence intervals were developed to estimate the true shopping expenditure, what differences would exist?
If 95% and 98% confidence intervals were developed to estimate the true shopping expenditure, what differences would exist?
(Multiple Choice)
4.7/5  (34)
(34)
College X is concerned about their employees making use of their email for non-business purposes. You have been approached to assist in this matter. College X decides on a 90% confidence level and state that the estimation proportion must be within 2 percent of the population proportion. A pilot survey reveals that 10 out of 50 emails sampled were not for business purposes. How many emails should be surveyed to meet your requirements?
(Multiple Choice)
4.9/5  (35)
(35)
The mean weight of trucks traveling on a particular section of Highway 401 is not known. A provincial highway inspector needs an estimate of the mean. He selects a random sample of 49 trucks passing the weighing station and finds the mean is 15.8 tons, with a standard deviation of the sample of 3.8 tons. What is the 95 percent interval for the population mean?
(Multiple Choice)
4.9/5  (38)
(38)
Recently, a university surveyed recent graduates of the English Department for their starting salaries. One hundred graduates returned the survey. The average salary was $35,000 with a standard deviation of $2,000. What is the best point estimate of the population mean?
(Multiple Choice)
4.7/5  (31)
(31)
The following summarizes the amount of snowfall in Ontario over the past number of years. 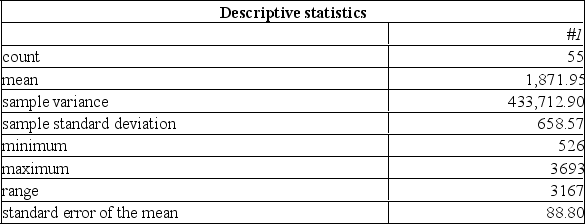 Determine a 98% confidence interval for the average annual snowfall.
Determine a 98% confidence interval for the average annual snowfall.
(Multiple Choice)
4.8/5  (36)
(36)
The Sugar Producers Association wants to estimate the mean yearly sugar consumption. A sample of 16 people reveals the mean yearly consumption to be 27 kg with a sample standard deviation of 9 kg. Assume a normal population. Develop a 99% confidence interval for the mean annual consumption of sugar.
(Multiple Choice)
4.7/5  (26)
(26)
How large a sample of government employees should be taken if we want to estimate with 98% confidence the mean salary to within $2,000? The population standard deviation is assumed to be $10,500. (Round up to the nearest whole number)
(Multiple Choice)
4.8/5  (37)
(37)
Showing 61 - 80 of 134
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)