Exam 10: Regression Analysis: Estimating Relationships
Exam 1: Introduction to Data Analysis and Decision Making30 Questions
Exam 2: Describing the Distribution of a Single Variable97 Questions
Exam 3: Finding Relationships Among Variables84 Questions
Exam 4: Probability and Probability Distributions113 Questions
Exam 5: Normal, binomial, poisson, and Exponential Distributions118 Questions
Exam 6: Decision Making Under Uncertainty106 Questions
Exam 7: Sampling and Sampling Distributions92 Questions
Exam 8: Confidence Interval Estimation85 Questions
Exam 9: Hypothesis Testing85 Questions
Exam 10: Regression Analysis: Estimating Relationships97 Questions
Exam 11: Regression Analysis: Statistical Inference87 Questions
Exam 12: Time Series Analysis and Forecasting104 Questions
Exam 13: Introduction to Optimization Modeling91 Questions
Exam 14: Optimization Modeling: Applications115 Questions
Exam 15: Introduction to Simulation Modeling81 Questions
Exam 16: Simulation Models104 Questions
Select questions type
A regression analysis between weight (Y in pounds)and height (X in inches)resulted in the following least squares line: 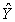 = 140 + 5X.This implies that if the height is increased by 1 inch,the weight is expected to increase on average by 5 pounds.
= 140 + 5X.This implies that if the height is increased by 1 inch,the weight is expected to increase on average by 5 pounds.
(True/False)
4.9/5  (31)
(31)
The percentage of variation explained 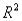 is the square of the correlation between the observed Y values and the fitted Y values.
is the square of the correlation between the observed Y values and the fitted Y values.
(True/False)
4.9/5  (41)
(41)
In simple linear regression,the divisor of the standard error of estimate 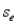 is n - 1; simply because there is only one explanatory variable of interest.
is n - 1; simply because there is only one explanatory variable of interest.
(True/False)
4.8/5  (43)
(43)
The coefficients for logarithmically transformed explanatory variables should be interpreted as the percent change in the dependent variable for a 1% percent change in the explanatory variable.
(True/False)
4.8/5  (35)
(35)
The adjusted R2 is adjusted for the number of explanatory variables in a regression equation,and it has he same interpretation as the standard R2.
(True/False)
4.8/5  (30)
(30)
(A)Use the information above to estimate the regression model.
(B)Interpret each of the estimated regression coefficients of the regression model in (A).
(C)Does using a non-linear model seem to be a good choice in this example? Explain your answer.
(Essay)
4.9/5  (39)
(39)
To help explain or predict the response variable in every regression study,we use one or more explanatory variables.These variables are also called response variables or independent variables.
(True/False)
4.8/5  (37)
(37)
Correlation is measured on a scale from 0 to 1,where 0 indicates no linear relationship between two variables,and 1 indicates a perfect linear relationship.
(True/False)
4.8/5  (34)
(34)
Obtain a residual plot vs.Service Interval.Does this affect your opinion of the validity of the model in Question 135?
(Essay)
4.9/5  (38)
(38)
Do you think this model proves the agency's point about maintenance? Explain your answer.
(Essay)
4.9/5  (32)
(32)
Interpret the model you developed in Question 139.Does it help you assess the agency's claim? What should the agency conclude about the relationship between service interval and maintenance costs?
(Essay)
4.8/5  (39)
(39)
(A)Is there evidence of a linear relationship between the selling price and the square footage of the homes? If so,interpret the least squares line and characterize the relationship (i.e.,positive,negative,strong,weak,etc.).
(B)Identify and interpret the coefficient of determination ( 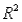 )for the model in (A).
(C)Identify and interpret the standard error of estimate
)for the model in (A).
(C)Identify and interpret the standard error of estimate 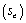 for the model in (A).
(D)Is there evidence of a linear relationship between the selling price and number of bedrooms of the homes? If so,interpret the least squares line and characterize the relationship (i.e.,positive,negative,strong,weak,etc.).
(E)Identify and interpret the coefficient of determination (
for the model in (A).
(D)Is there evidence of a linear relationship between the selling price and number of bedrooms of the homes? If so,interpret the least squares line and characterize the relationship (i.e.,positive,negative,strong,weak,etc.).
(E)Identify and interpret the coefficient of determination ( 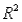 )for the model in (D).
(F)Identify and interpret the standard error of the estimate (
)for the model in (D).
(F)Identify and interpret the standard error of the estimate ( 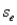 )for the model in (C).
(G)Which of the two variables,the square footage or the number of bedrooms,is the relationship with home selling price stronger? Justify your choice.
)for the model in (C).
(G)Which of the two variables,the square footage or the number of bedrooms,is the relationship with home selling price stronger? Justify your choice.
(Essay)
4.9/5  (41)
(41)
When the scatterplot appears as a shapeless swarm of points,this can indicate that there is no relationship between the response variable Y and the explanatory variable X,or at least none worth pursuing.
(True/False)
4.9/5  (33)
(33)
Data collected from approximately the same period of time from a cross-section of a population are called:
(Multiple Choice)
4.9/5  (44)
(44)
(A)Use the information above to estimate the linear regression model.
(B)Write the regression equation in (A)as two separate equations; one for females and one for males,and interpret the results.
(C)Would any of the variables in the linear regression model in (A)be considered a dummy variable? Explain your answer.
(D)Identify and interpret the coefficient of determination ( 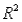 )for the model in (A).
(E)Identify and interpret the standard error of estimate (se)for the model in (A).
)for the model in (A).
(E)Identify and interpret the standard error of estimate (se)for the model in (A).
(Essay)
4.8/5  (38)
(38)
In a multiple regression analysis with three explanatory variables,suppose that there are 60 observations and the sum of the residuals squared is 28.The standard error of estimate must be 0.7071.
(True/False)
4.9/5  (28)
(28)
In a simple regression analysis,if the standard error of estimate 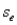 = 15 and the number of observations n = 10,then the sum of the residuals squared must be 120.
= 15 and the number of observations n = 10,then the sum of the residuals squared must be 120.
(True/False)
4.9/5  (38)
(38)
An important condition when interpreting the coefficient for a particular independent variable X in a multiple regression equation is that:
(Multiple Choice)
4.8/5  (38)
(38)
The covariance is not used as much as the correlation because
(Multiple Choice)
4.8/5  (34)
(34)
Showing 21 - 40 of 97
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)