Exam 10: Regression Analysis: Estimating Relationships
Exam 1: Introduction to Data Analysis and Decision Making30 Questions
Exam 2: Describing the Distribution of a Single Variable97 Questions
Exam 3: Finding Relationships Among Variables84 Questions
Exam 4: Probability and Probability Distributions113 Questions
Exam 5: Normal, binomial, poisson, and Exponential Distributions118 Questions
Exam 6: Decision Making Under Uncertainty106 Questions
Exam 7: Sampling and Sampling Distributions92 Questions
Exam 8: Confidence Interval Estimation85 Questions
Exam 9: Hypothesis Testing85 Questions
Exam 10: Regression Analysis: Estimating Relationships97 Questions
Exam 11: Regression Analysis: Statistical Inference87 Questions
Exam 12: Time Series Analysis and Forecasting104 Questions
Exam 13: Introduction to Optimization Modeling91 Questions
Exam 14: Optimization Modeling: Applications115 Questions
Exam 15: Introduction to Simulation Modeling81 Questions
Exam 16: Simulation Models104 Questions
Select questions type
Which of the following is an example of a nonlinear regression model?
(Multiple Choice)
4.8/5  (47)
(47)
(A)Use the information above to estimate the linear regression model.
(B)Interpret each of the estimated regression coefficients of the regression model in (A).
(C)Identify and interpret the coefficient of determination ( 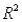 ),for the model in (A).
(D)Identify and interpret the adjusted
),for the model in (A).
(D)Identify and interpret the adjusted 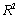 for the model in (A).
for the model in (A).
(Essay)
4.9/5  (42)
(42)
In multiple regression,the coefficients reflect the expected change in:
(Multiple Choice)
5.0/5  (36)
(36)
If the regression equation includes anything other than a constant plus the sum of products of constants and variables,the model will not be linear
(True/False)
4.8/5  (38)
(38)
(A)Estimate a simple linear regression model with Service Interval (X)and Maintenance Cost (Y).Interpret the slope coefficient of the least squares line as well as the computed value of 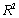 .
(B)Do you think this model proves the agency's point about maintenance? Explain your answer.
(C)Obtain a residual plot vs.Service Interval.Does this affect your opinion of the validity of the model in (A)?
(D)Obtain a scatterplot of Maintenance Cost vs.Service Interval.Does this affect your opinion of the validity of the model in (A)?
(E)Use what you have learned about transformations to fit an alternative model to the one in (A).
(F)Interpret the model you developed in (E).Does it help you assess the agency's claim? What should the agency conclude about the relationship between service interval and maintenance costs?
.
(B)Do you think this model proves the agency's point about maintenance? Explain your answer.
(C)Obtain a residual plot vs.Service Interval.Does this affect your opinion of the validity of the model in (A)?
(D)Obtain a scatterplot of Maintenance Cost vs.Service Interval.Does this affect your opinion of the validity of the model in (A)?
(E)Use what you have learned about transformations to fit an alternative model to the one in (A).
(F)Interpret the model you developed in (E).Does it help you assess the agency's claim? What should the agency conclude about the relationship between service interval and maintenance costs?
(Essay)
4.7/5  (31)
(31)
In a simple regression with a single explanatory variable,the multiple R is the same as the standard correlation between the Y variable and the explanatory X variable.
(True/False)
4.8/5  (36)
(36)
A regression analysis between sales (in $1000)and advertising (in $100)resulted in the following least squares line: 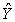 = 84 +7X.This implies that if there is no advertising,then the predicted amount of sales (in dollars)is $84,000.
= 84 +7X.This implies that if there is no advertising,then the predicted amount of sales (in dollars)is $84,000.
(True/False)
4.8/5  (36)
(36)
The primary purpose of a nonlinear transformation is to "straighten out" the data on a scatterplot
(True/False)
4.7/5  (40)
(40)
(A)Estimate a simple linear regression model involving shipping cost and package weight.Interpret the slope coefficient of the least squares line as well as the computed value of 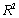 .
(B)Add another explanatory variable - distance shipped - to the regression to (A).Estimate and interpret this expanded model.How does the
.
(B)Add another explanatory variable - distance shipped - to the regression to (A).Estimate and interpret this expanded model.How does the 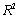 value for this multiple regression model compare to that of the simple regression model estimated in (A)? Explain any difference between the two
value for this multiple regression model compare to that of the simple regression model estimated in (A)? Explain any difference between the two 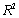 values.Compute and interpret the adjusted
values.Compute and interpret the adjusted 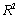 value for the revised model.
(C)Suppose that one of the managers of this express delivery service company is trying to decide whether to add an interaction term involving the package weight
value for the revised model.
(C)Suppose that one of the managers of this express delivery service company is trying to decide whether to add an interaction term involving the package weight 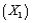 and the distance shipped
and the distance shipped 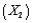 in the multiple regression model developed previously.Why would the manager want to add such a term to the regression equation?
(D)Estimate the revised model using the interaction term suggested in (C).
(E)Interpret each of the estimated coefficients in your revised model in (D).In particular,how do you interpret the coefficient for the interaction term in the revised model?
(F)Does this revised model in (D)fit the given data better than the original multiple regression model in (B)? Explain why or why not.
in the multiple regression model developed previously.Why would the manager want to add such a term to the regression equation?
(D)Estimate the revised model using the interaction term suggested in (C).
(E)Interpret each of the estimated coefficients in your revised model in (D).In particular,how do you interpret the coefficient for the interaction term in the revised model?
(F)Does this revised model in (D)fit the given data better than the original multiple regression model in (B)? Explain why or why not.
(Essay)
4.8/5  (30)
(30)
(A)Use the information above to estimate the linear regression model.
(B)Interpret each of the estimated regression coefficients of the regression model in (A).
(C)Would any of the variables in this model be considered a dummy variable? Explain your answer.
(D)Identify and interpret the coefficient of determination ( 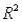 )and the standard error of the estimate (se)for the model in (A).
(E)Use the estimated model in (A)to predict the sales price of a 2500 square feet,15-year old house that has 5 rooms and an attached garage.
)and the standard error of the estimate (se)for the model in (A).
(E)Use the estimated model in (A)to predict the sales price of a 2500 square feet,15-year old house that has 5 rooms and an attached garage.
(Essay)
4.7/5  (35)
(35)
In a simple linear regression problem,if the percentage of variation explained 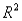 is 0.95,this means that 95% of the variation in the explanatory variable X can be explained by regression.
is 0.95,this means that 95% of the variation in the explanatory variable X can be explained by regression.
(True/False)
4.7/5  (37)
(37)
In regression analysis,if there are several explanatory variables,it is called:
(Multiple Choice)
4.9/5  (36)
(36)
Correlation is used to determine the strength of the linear relationship between an explanatory variable X and response variable Y.
(True/False)
4.8/5  (39)
(39)
In a simple linear regression analysis,the following sums of squares are produced: 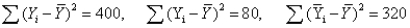 The proportion of the variation in Y that is explained by the variation in X is:
The proportion of the variation in Y that is explained by the variation in X is:
(Multiple Choice)
4.9/5  (45)
(45)
The least squares line is the line that minimizes the sum of the residuals.
(True/False)
4.8/5  (40)
(40)
A regression analysis between sales (in $1000)and advertising (in $100)resulted in the following least squares line: 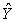 = 84 +7X.This implies that if advertising is $800,then the predicted amount of sales (in dollars)is $140,000.
= 84 +7X.This implies that if advertising is $800,then the predicted amount of sales (in dollars)is $140,000.
(True/False)
4.7/5  (36)
(36)
Showing 41 - 60 of 97
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)