Exam 11: Rolling, Torque, and Angular Momentum
Exam 1: Measurement37 Questions
Exam 2: Motion Along a Straight Line90 Questions
Exam 3: Vector37 Questions
Exam 4: Motion in Two and Three Dimensions56 Questions
Exam 5: Force and Motion I73 Questions
Exam 6: Force and Motion II74 Questions
Exam 7: Kinetic Energy and Work73 Questions
Exam 8: Potential Energy and Conservation of Energy63 Questions
Exam 9: Center of Mass and Linear Momentum99 Questions
Exam 10: Rotation102 Questions
Exam 11: Rolling, Torque, and Angular Momentum66 Questions
Exam 12: Equilibrium and Elasticity57 Questions
Exam 13: Gravitation55 Questions
Exam 14: Fluids88 Questions
Exam 15: Oscillations75 Questions
Exam 16: Waves I82 Questions
Exam 17: Waves II71 Questions
Exam 18: Temperature, Heat, and the First Law of Thermodynamics96 Questions
Exam 19: The Kinetic Theory of Gases113 Questions
Exam 20: Entropy and the Second Law of Thermodynamics61 Questions
Exam 21: Electric Charge52 Questions
Exam 22: Electric Fields55 Questions
Exam 23: Gauss Law38 Questions
Exam 24: Electric Potential52 Questions
Exam 25: Capacitance61 Questions
Exam 26: Current and Resistance55 Questions
Exam 27: Circuits73 Questions
Exam 28: Magnetic Fields55 Questions
Exam 29: Magnetic Fields Due to Currents49 Questions
Exam 30: Induction and Inductance90 Questions
Exam 31: Electromagnetic Oscillations and Alternating Current88 Questions
Exam 32: Maxwells Equations; Magnetism of Matter81 Questions
Exam 33: Electromagnetic Waves83 Questions
Exam 34: Images79 Questions
Exam 35: Interference46 Questions
Exam 36: Diffraction77 Questions
Exam 37: Relativity68 Questions
Exam 38: Photons and Matter Waves57 Questions
Exam 39: More About Matter Waves41 Questions
Exam 40: All About Atoms79 Questions
Exam 41: Conduction of Electricity in Solids51 Questions
Exam 42: Nuclear Physics68 Questions
Exam 43: Energy From the Nucleus50 Questions
Exam 44: Quarks, Leptons, and the Big Bang55 Questions
Select questions type
A 2.0-kg block travels around a 0.50-m radius circle with an angular velocity of 12 rad/s. The magnitude of its angular momentum about the center of the circle is:
(Multiple Choice)
4.9/5  (39)
(39)
Two wheels roll side-by-side without sliding, at the same speed. The radius of wheel 2 is twice the radius of wheel 1. The angular velocity of wheel 2 is:
(Multiple Choice)
4.9/5  (31)
(31)
A 2.0-kg stone is tied to a 0.50-m long string and swung around a circle at a constant angular velocity of 12 rad/s. The net torque on the stone about the center of the circle is:
(Multiple Choice)
4.8/5  (39)
(39)
Two objects are moving in the x, y plane as shown. The magnitude of their total angular momentum (about the origin O) is: 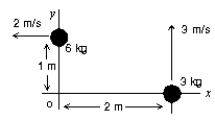
(Multiple Choice)
4.8/5  (39)
(39)
A wheel, with rotational inertia I, mounted on a vertical shaft with negligible rotational inertia, is rotating with angular speed 0. A nonrotating wheel with rotational inertia 2I is suddenly dropped onto the same shaft as shown. The resultant combination of the two wheels and shaft will rotate at: 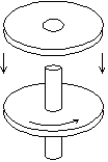
(Multiple Choice)
4.9/5  (31)
(31)
A hoop rolls with constant velocity and without sliding along level ground. Its rotational kinetic energy is:
(Multiple Choice)
4.9/5  (35)
(35)
Two objects are moving in the x, y plane as shown. If a net torque of 44 N∙m acts on them for 5.0 seconds, what is the change in their angular momentum? 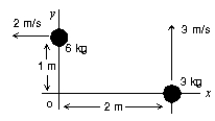
(Multiple Choice)
4.7/5  (29)
(29)
A pulley with radius R and rotational inertia I is free to rotate on a horizontal fixed axis through its center. A string passes over the pulley. A block of mass m1 is attached to one end and a block of mass m2, is attached to the other. At one time the block with mass m1 is moving downward with speed v. If the string does not slip on the pulley, the magnitude of the total angular momentum, about the pulley center, of the blocks and pulley, considered as a system, is given by:
(Multiple Choice)
4.8/5  (34)
(34)
A force 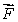 = 4.2 N + 3.7 N + 1.2 N acts on a particle located at x = 3.3 m. What is the torque on the particle around the origin?
= 4.2 N + 3.7 N + 1.2 N acts on a particle located at x = 3.3 m. What is the torque on the particle around the origin?
(Multiple Choice)
4.8/5  (32)
(32)
When a man on a frictionless rotating stool extends his arms horizontally, his rotational kinetic energy:
(Multiple Choice)
4.9/5  (44)
(44)
A thin-walled hollow tube rolls without sliding along the floor. The ratio of its translational kinetic energy to its rotational kinetic energy (about an axis through its center of mass) is:
(Multiple Choice)
4.9/5  (29)
(29)
When we apply the energy conversation principle to a cylinder rolling down an incline without sliding, we exclude the work done by friction because:
(Multiple Choice)
4.9/5  (37)
(37)
A 5.0-kg ball rolls without sliding from rest down an inclined plane. A 4.0-kg block, mounted on roller bearings totaling 100 g, rolls from rest down the same plane. At the bottom, the block has:
(Multiple Choice)
4.8/5  (37)
(37)
The coefficient of static friction between a certain cylinder and a horizontal floor is 0.40. If the rotational inertia of the cylinder about its symmetry axis is given by I = (1/2)MR2, then the maximum acceleration the cylinder can have without sliding is:
(Multiple Choice)
4.9/5  (46)
(46)
A particle moves along the x axis. In order to calculate the angular momentum of the particle, you need to know:
(Multiple Choice)
4.7/5  (32)
(32)
Two pendulum bobs of unequal mass are suspended from the same fixed point by strings of equal length. The lighter bob is drawn aside and then released so that it collides with the other bob on reaching the vertical position. The collision is elastic. What quantities are conserved in the collision?
(Multiple Choice)
4.8/5  (28)
(28)
A 6.0-kg particle moves to the right at 4.0 m/s as shown. The magnitude of its angular momentum about the point O is: 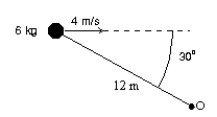
(Multiple Choice)
4.9/5  (44)
(44)
A 2.0-kg block travels around a 0.50-m radius circle with an angular speed of 12 rad/s. The circle is parallel to the xy plane and is centered on the z axis, 0.75 m from the origin. The component in the xy plane of the angular momentum around the origin has magnitude:
(Multiple Choice)
4.8/5  (39)
(39)
Showing 41 - 60 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)