Exam 12: Computer Simulation: Basic Concepts
Exam 1: Introduction54 Questions
Exam 2: Linear Programming: Basic Concepts85 Questions
Exam 3: Linear Programming: Formulation and Applications76 Questions
Exam 4: The Art of Modeling With Spreadsheets75 Questions
Exam 5: What-If Analysis for Linear Programming75 Questions
Exam 6: Network Optimization Problems84 Questions
Exam 7: Using Binary Integer Programming to Deal With Yes-Or-No Decisions76 Questions
Exam 8: Nonlinear Programming75 Questions
Exam 9: Decision Analysis80 Questions
Exam 10: Forecasting77 Questions
Exam 11: Queueing Models78 Questions
Exam 12: Computer Simulation: Basic Concepts79 Questions
Exam 13: Computer Simulation With Analytic Solver77 Questions
Select questions type
The main reason that a large number of replications of a simulation would be made is:
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
C
Note: This question requires the use of the Queueing Simulator spreadsheet in Excel. Use the queueing simulator to simulate a queueing system with 2 servers, exponential interarrival times with a mean of 20 seconds and constant service times of 35 seconds. Use a simulation run length of 10,000 arrivals. What is the point estimate for the average number of customers in the system?
Free
(Multiple Choice)
4.7/5  (34)
(34)
Correct Answer:
B
One purpose of running experiments on a simulation model is to answer "what-if" questions.
Free
(True/False)
4.9/5  (38)
(38)
Correct Answer:
True
The Queueing Simulator returned the results shown below for a system with 2 servers. Which of the following is most likely to occur? 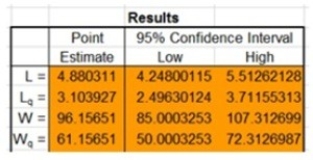
(Multiple Choice)
4.9/5  (36)
(36)
After reviewing past history, you have assembled the following table showing the frequency of certain levels of sales over the past 40 months. If the smallest random number used to represent sales of 200 units is 0.45, what will be the largest number used to represent sales of 200 units?
Sales (units) Frequency Corregonding Randam Numbers 100 12 150 6 200 8 0.45\leqx
(Multiple Choice)
4.9/5  (34)
(34)
If a simulation begins with the first random number, the third simulated value would be:
Random numbers: 0.6246, 0.2594, 0.4055
Demand Frequency 0 0.15 1 0.30 2 0.25 3 0.15 4 0.15
(Multiple Choice)
4.8/5  (42)
(42)
The Queueing Simulator returned the results shown below for a system with 3 servers. If the firm would like their waiting room to be full no more than 2% of the time, how large must their waiting room be? 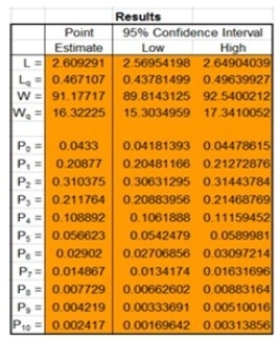
(Multiple Choice)
4.7/5  (42)
(42)
Computer simulation is only applicable to situations that have elements that can be described by random variables
(True/False)
4.7/5  (26)
(26)
You have determined that waiting times at a toll booth are uniformly distributed over the interval 20 to 60 seconds. What formula would you use in Excel to generate random values in this range that follow the uniform distribution?
(Multiple Choice)
4.8/5  (42)
(42)
You have determined that waiting times at a restaurant are uniformly distributed over the interval 5 to 12 minutes. What formula would you use in Excel to generate random values in this range that follow the uniform distribution?
(Multiple Choice)
4.7/5  (40)
(40)
The main procedure for advancing the time on the simulation clock is called next-event time advance.
(True/False)
4.8/5  (45)
(45)
After reviewing past history, you have assembled the following table showing the frequency of certain levels of sales over the past 40 months. If the smallest random number used to represent sales of 100 units is 0, what will be the largest number used to represent sales of 100 units?
Sales (units) Frequency Carrespmeming Random Numbers 100 12 0\leqx
(Multiple Choice)
4.9/5  (38)
(38)
Analytical methods are preferable to simulation if an appropriate analytic method is available.
(True/False)
4.7/5  (29)
(29)
Managers can use simulation to obtain optimal answers for a wide range of problems.
(True/False)
4.9/5  (31)
(31)
Random observations can be generated in Excel by using the VLOOKUP function.
(True/False)
4.8/5  (34)
(34)
Note: This question requires the use of the Queueing Simulator spreadsheet in Excel. Use the queueing simulator to simulate a queueing system with 2 servers, exponential interarrival times with a mean of 20 seconds and constant service times of 35 seconds. Use a simulation run length of 10,000 arrivals. If you observe the system at a random time, what is the probability that there will be 3 or more customers waiting in line?
(Multiple Choice)
4.9/5  (33)
(33)
You have determined that waiting times at a restaurant are uniformly distributed over the interval 5 to 12 minutes. The first random number your simulation returns is 0.2154. What is the waiting time that this random number generates?
(Multiple Choice)
4.9/5  (33)
(33)
Note: This question requires the use of the Queueing Simulator spreadsheet in Excel. Use the queueing simulator to simulate a queueing system with 3 servers, uniform interarrival times between 20 and 50 seconds and exponential service times with an average of 75 seconds. Use a simulation run length of 10,000 arrivals. What is the point estimate for the total amount of time a customer will spend in the system?
(Multiple Choice)
4.8/5  (39)
(39)
Showing 1 - 20 of 79
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)