Exam 6: Network Optimization Problems

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 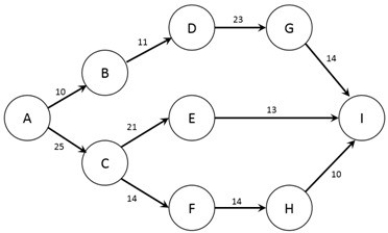How many transshipment nodes are present in this problem?

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 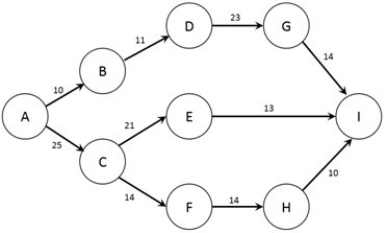What is the capacity of the connection between nodes F and H?

All network optimization problems actually are special types of linear programming problems.

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M. 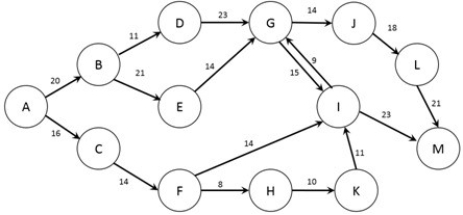Note: This question requires Solver. Formulate the problem in Solver and find the optimal solution. Which of the following nodes are not visited?

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below: \text{Customer (requirement)}\\ \begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\ \text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array} How many demand nodes are present in this problem?

The figure below shows the possible routes from city A to city J as well as the time (in minutes) required for a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the quickest option to travel from city A to city J. 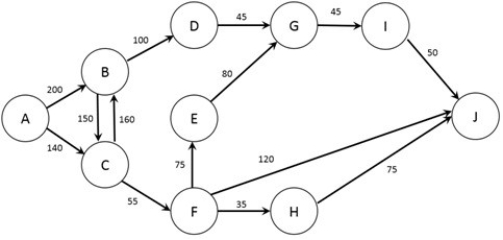Which type of network optimization problem is used to solve this problem?

The model for any minimum cost flow problem is represented by a network with flow passing through it.

The figure below shows the possible routes from city A to city M as well as the cost (in dollars) of a trip between each pair of cities (note that if no arc joins two cities it is not possible to travel non-stop between those two cities). A traveler wishes to find the lowest cost option to travel from city A to city M.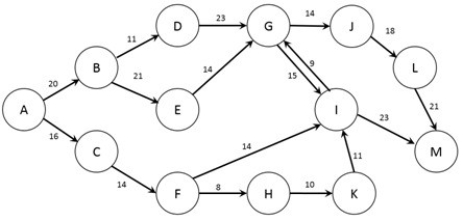 Which type of network optimization problem is used to solve this problem?

Shortest path problems are concerned with finding the shortest route through a network.

As long as all its supplies and demands have integer values, any minimum cost flow problem is guaranteed to have an optimal solution with integer values.

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 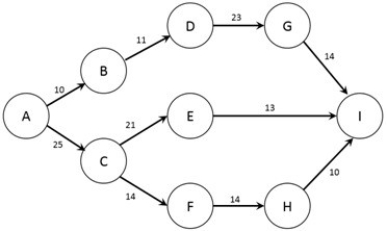Which type of network optimization problem is used to solve this problem?

A minimum cost flow problem is a special type of:

Which of the following will have negative net flow in a minimum cost flow problem?

In a maximum flow problem, the source and sink have fixed supplies and demands.

The figure below shows the nodes (A-I) and capacities (labelled on arcs in TB/s) of a computer network. The firm would like to know how much information can flow from node A to node I. 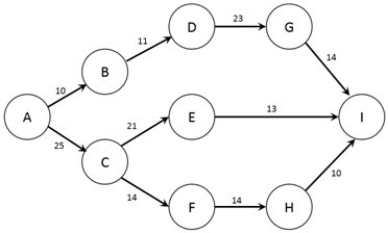Note: This question requires Solver. Formulate the problem in Solver and find the optimal solution. What is the maximum amount of data that can be transmitted from node A to node I?

Which of the following is an application of a shortest path problem? I. Minimize total distance traveled. II. Minimize total flow through a network. III. Minimize total cost of a sequence of activities. IV. Minimize total time of a sequence of activities

What is the objective of a maximum flow problem?

A manufacturing firm has three plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below: \text{Customer (requirement)}\\ \begin{array} { l c c c c } &&&Customer ~3 &Customer ~4\\ \text { Factory (capacity) } & \text { Custcmer } 1 ( 25 ) & \text { Customer } 2 ( 50 ) & ( 125 ) & ( 75 ) \\ \text { A (100) } & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ B ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \text { C (100) } & \$ 22 & \$ 20 & \$ 25 & \$ 14 \end{array} How many arcs will the network have?

Which of the following can be used to optimally solve minimum cost flow problems? I. The simplex method. II. The network simplex method. III. A greedy algorithm.

A manufacturing firm has four plants and wants to find the most efficient means of meeting the requirements of its four customers. The relevant information for the plants and customers, along with shipping costs in dollars per unit, are shown in the table below: \text{Customer (requirement)}\\ \begin{array} { l c c c c } &&Customer ~2 &Customer ~3& Customer ~4\\ \text { Factory (capacity)}&\text{ Customer } 1 ( 125 ) & ( 150 ) & ( 175 ) & ( 75 ) \\ A ( 100 ) & \$ 15 & \$ 10 & \$ 20 & \$ 17 \\ \mathrm {~B} ( 75 ) & \$ 20 & \$ 12 & \$ 19 & \$ 20 \\ \mathrm { C } ( 100 ) & \$ 22 & \$ 20 & \$ 25 & \$ 14 \\ \mathrm { D } ( 250 ) & \$ 21 & \$ 15 & \$ 28 & \$ 12 \end{array} How many arcs will the network have?