Exam 4: Linear Programming: an Algebraic Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Use the simplex method for solving nonstandard problems to solve the given linear programming problem. 
(Multiple Choice)
4.7/5  (41)
(41)
Consider the linear programming problem. 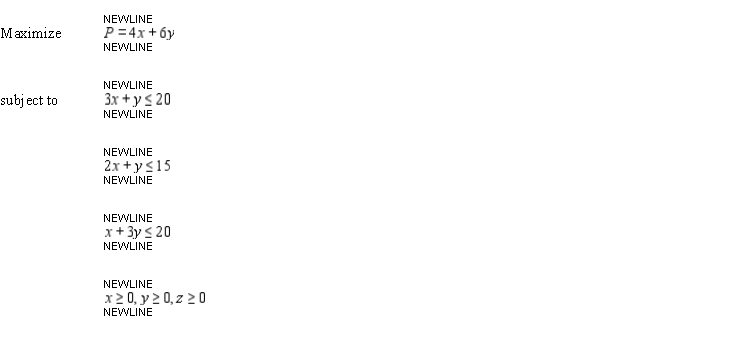 Sketch the feasible set for the linear programming problem.
Sketch the feasible set for the linear programming problem.
(Multiple Choice)
5.0/5  (40)
(40)
Ashley has earmarked at most $200,000 for investment in three mutual funds: a money market fund, an international equity fund, and a growth-and-income fund. The money market fund has a rate of return of 6%/year, the international equity fund has a rate of return of 9%/year, and the growth-and-income fund has a rate of return of 16%/year. Ashley has stipulated that no more than 25% of her total portfolio should be in the growth-and-income fund and that no more than 50% of her total portfolio should be in the international equity fund. To maximize the return on her investment, how much should Ashley invest in each type of fund?
$ __________ in the money market fund, $ __________ in the international equity fund,
$ __________ in the growth-and-income fund
What is the maximum return? $ __________
(Essay)
4.8/5  (31)
(31)
Solve the linear programming problem by the simplex method. 
(Multiple Choice)
4.8/5  (30)
(30)
Use the simplex method for solving nonstandard problems to solve the given linear programming problem. 
(Multiple Choice)
4.8/5  (30)
(30)
Find the pivot element to be used in the next iteration of the simplex method. 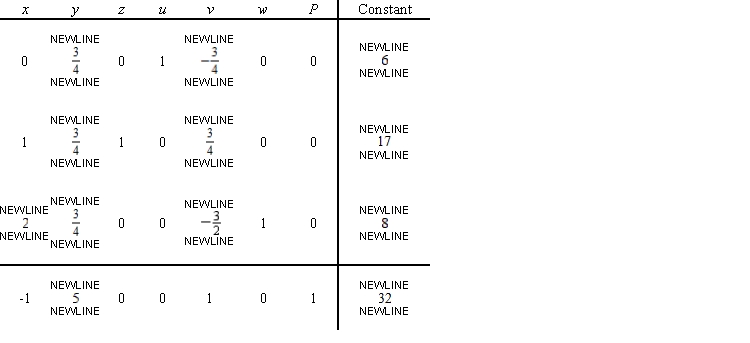
(Multiple Choice)
4.8/5  (23)
(23)
A nutritionist at the Medical Center has been asked to prepare a special diet for certain patients. He has decided that the meals should contain a minimum of 210 mg of calcium,9 mg of iron, and 30 mg of vitamin C. He has further decided that the meals are to be prepared from foods A and B. Each ounce of food A contains 20 mg of calcium, 1 mg of iron, 2 mg of vitamin C, and 2 mg of cholesterol. Each ounce of food B contains 15 mg of calcium, 0.5 mg of iron, 3 mg of vitamin C, and 3 mg of cholesterol.
Determine how many ounces of each type of food the nutritionist should use in a meal so that the cholesterol content is minimized and the minimum requirements of calcium, iron, and vitamin C are met.
(Essay)
4.9/5  (38)
(38)
As part of a campaign to promote its annual clearance sale, a company decided to buy television-advertising time on a TV station. Company's television-advertising budget is $102,000. Morning time costs $3,000/minute, afternoon time costs $1,000/minute, and evening (prime) time costs $12,000/minute. Because of previous commitments, the station cannot offer the company more than 7 min of prime time or more than a total of 25 min of advertising time over the 4 wk in which the commercials are to be run. The station estimates that morning commercials are seen by 210,000 people, afternoon commercials are seen by 105,000 people, and evening commercials are seen by 630,000 people. How much morning, afternoon, and evening advertising time should the company buy to maximize exposure of its commercials? What is the maximum number of viewers?
(Multiple Choice)
4.8/5  (32)
(32)
Check that the given simplex tableau is in final form. Find the solution to the associated regular linear programming problem. 
(Multiple Choice)
4.9/5  (36)
(36)
Solve the linear programming problem by the simplex method. 
(Multiple Choice)
4.8/5  (27)
(27)
The owner of the Health JuiceBar wishes to prepare a low-calorie fruit juice with a high vitamin-A and -C content by blending orange juice and pink grapefruit juice. Each glass of the blended juice is to contain at least 1,260 International Units (IU) of vitamin A and 184 IU of vitamin C. One ounce of orange juice contains 70 IU of vitamin A, 18 IU of vitamin C, and 13 calories; each ounce of pink grapefruit juice contains 140 IU of vitamin A, 16 IU of vitamin C, and 12 calories. How many ounces of each juice should a glass of the blend contain if it is to meet the minimum vitamin requirements while containing a minimum number of calories?
(Multiple Choice)
4.9/5  (39)
(39)
Find the solution to the associated regular linear programming problem. 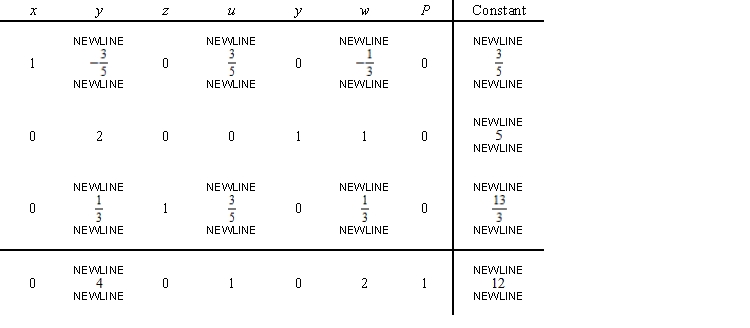
(Multiple Choice)
4.9/5  (29)
(29)
Use the Simplex Method for Solving Nonstandard Problems to solve the linear programming problem. 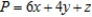
(Multiple Choice)
4.8/5  (31)
(31)
Steinwelt Piano manufactures uprights and consoles in two plants, plant I and plant II. The output of plant I is at most 210 pianos/month, whereas the output of plant II is at most 175 pianos/month. These pianos are shipped to three warehouses that serve as distribution centers for the company. To fill current and projected orders, warehouse A requires a minimum of 140 pianos/month, warehouse B requires at least 105 pianos/month, and warehouse C requires at least 140 pianos/month. The shipping cost of each piano from plant I to warehouse A, warehouse B, and warehouse C is $60, $60, and $80, respectively, and the shipping cost of each piano from plant II to warehouse A, warehouse B, and warehouse C is $90, $70, and $50, respectively. Use the method of this section to determine the shipping schedule that will enable Steinwelt to meet the warehouses' requirements while keeping the shipping costs to a minimum.
(Multiple Choice)
4.8/5  (31)
(31)
National Business Machines Corporation manufactures two models of fax machines: A and B. Each model A costs $110 to make, and each model B costs $130. The profits are $30 for each model A and $40 for each model B fax machine. If the total number of fax machines demanded each month does not exceed 2,500 and the company has earmarked no more than $600,000/month for manufacturing costs, find how many units of each model National should make each month in order to maximize its monthly profits.
__________ units of model A, __________ units of model B
What is the largest monthly profit the company can make? $ __________
(Essay)
4.8/5  (35)
(35)
Steinwelt Piano manufactures uprights and consoles in two plants, plant I and plant II. The output of plant I is at most 180 pianos/month, whereas the output of plant II is at most 150 pianos/month. These pianos are shipped to three warehouses that serve as distribution centers for the company. To fill current and projected orders, warehouse A requires a minimum of 120 pianos/month, warehouse B requires at least 90 pianos/month, and warehouse C requires at least 120 pianos/month. The shipping cost of each piano from plant I to warehouse A, warehouse B, and warehouse C is $60, $60, and $80, respectively, and the shipping cost of each piano from plant II to warehouse A, warehouse B, and warehouse C is $80, $70, and $50, respectively.
Use the method of this section to determine the shipping schedule that will enable Steinwelt to meet the warehouses' requirements while keeping the shipping costs to a minimum.
__________ pianos from plant I to warehouse A
__________ pianos from plant I to warehouse B
__________ pianos from plant I to warehouse C
__________ pianos from plant II to warehouse A
__________ pianos from plant II to warehouse B
__________ pianos from plant II to warehouse C
(Essay)
4.8/5  (35)
(35)
Solve the linear programming problem by the simplex method. 
(Multiple Choice)
4.8/5  (29)
(29)
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
If a standard minimization linear programming problem has a unique solution, then so does the corresponding maximization problem with objective function 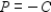 , where
, where 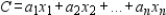 is the objective function for the minimization problem.
is the objective function for the minimization problem.
(True/False)
4.8/5  (37)
(37)
A company manufactures products A, B, and C. Each product is processed in three departments: I, II, and III. The total available labor-hours per week for departments I, II, and III are 930, 1,060, and 840, respectively. The time requirements (in hours/unit) and the profit per unit for each product are as follows:  If management decides that the number of units of product B manufactured must equal or exceed the number of units of products A and C manufactured, how many units of each product should the company produce in order to maximize its profit?
If management decides that the number of units of product B manufactured must equal or exceed the number of units of products A and C manufactured, how many units of each product should the company produce in order to maximize its profit?
(Multiple Choice)
4.7/5  (32)
(32)
Showing 21 - 40 of 115
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)