Exam 4: Linear Programming: an Algebraic Approach
Exam 1: Straight Lines and Linear Functions268 Questions
Exam 2: Systems of Linear Equations and Matrices313 Questions
Exam 3: Linear Programming: a Geometric Approach214 Questions
Exam 4: Linear Programming: an Algebraic Approach115 Questions
Exam 5: Mathematics of Finance207 Questions
Exam 6: Sets and Counting196 Questions
Exam 7: Probability273 Questions
Exam 8: Probability Distributions and Statistics263 Questions
Exam 9: Markov Chains and the Theory of Games203 Questions
Select questions type
Check that the given simplex tableau is in final form. Find the solution to the associated regular linear programming problem. 
(Multiple Choice)
5.0/5  (31)
(31)
Determine wheather the given simplex table is in the final form. If so, find the solution to the associated regular linear programming problem. 
(Multiple Choice)
4.9/5  (24)
(24)
Consider the linear programming problem.  Sketch the feasible set for the linear programming problem.
Sketch the feasible set for the linear programming problem.
(Multiple Choice)
4.8/5  (37)
(37)
Use the simplex method for solving nonstandard problems to solve the given linear programming problem. 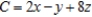
(Multiple Choice)
4.9/5  (33)
(33)
As part of a campaign to promote its annual clearance sale, a company decided to buy television-advertising time on a TV station. Company's television-advertising budget is $102,000. Morning time costs $3,000/minute, afternoon time costs $1,000/minute, and evening (prime) time costs $12,000/minute. Because of previous commitments, the station cannot offer the company more than 7 min of prime time or more than a total of 25 min of advertising time over the 3 wk in which the commercials are to be run. The station estimates that morning commercials are seen by 160,000 people, afternoon commercials are seen by 80,000 people, and evening commercials are seen by 480,000 people. How much morning, afternoon, and evening advertising time should the company buy to maximize exposure of its commercials?
__________ min of morning advertising time,
__________ min of afternoon advertising time,
__________ min of evening advertising time
What is the maximum number of viewers? Round your answer to two decimal places, if necessary.
__________ million viewers
(Essay)
4.9/5  (30)
(30)
Use the Simplex Method for Solving Nonstandard Problems to solve the linear programming problem. 
(Essay)
4.8/5  (35)
(35)
A pharmaceutical company produces three kinds of cold formulas: I, II, and III. It takes 5 hr to produce 1,000 bottles of formula I, 4 hr to produce 1,000 bottles of formula II, and 3 hr to produce 1,000 bottles of formula III. The profits for each 1,000 bottles of formula I, formula II, and formula III are $240, $170, and $210, respectively. Suppose, for a certain production run, there are enough ingredients on hand to make at most 7,000 bottles of formula I, 13,000 bottles of formula II, and 6,000 bottles of formula III. Furthermore, suppose the time for the production run is limited to a maximum of 90 hr. How many bottles of each formula should be produced in this production run so that the profit is maximized? What is the maximum profit realizable by the company? Are there any resources left over?
(Multiple Choice)
4.8/5  (31)
(31)
A farmer has 150 acres of land suitable for cultivating crops A and B. The cost of cultivating crop A is $40/acre and that of crop B is $60/acre. The farmer has a maximum of $7,600 available for land cultivation. Each acre of crop A requires 20 labor-hours, and each acre of crop B requires 25 labor-hours. The farmer has a maximum of 3,200 labor-hours available. He has also decided that he will cultivate at least 70 acres of crop A.
If he expects to make a profit of $170/acre on crop A and $230/acre on crop B, how many acres of each crop should he plant in order to maximize his profit?
__________ acres of crop A
__________ acres of crop B
Maximum profit is $__________.
(Essay)
4.9/5  (31)
(31)
Solve the linear programming problem by the simplex method. 
(Multiple Choice)
4.8/5  (40)
(40)
Solve the linear programming problem by the simplex method. 
(Multiple Choice)
4.9/5  (31)
(31)
Natsano has at most $60,000 to invest in the common stocks of two companies. He estimates that an investment in company A will yield a return of 10%, whereas an investment in company B, which he feels is a riskier investment, will yield a return of 20%. If he decides that his investment in the stocks of company A is to exceed his investment in the stocks of company B by at least $30,000, determine how much he should invest in the stocks of each company in order to maximize the returns on his investment.
(Multiple Choice)
4.8/5  (36)
(36)
Use the Simplex Method for Solving Nonstandard Problems to solve the linear programming problem. 
(Essay)
4.8/5  (37)
(37)
Use the simplex method for solving nonstandard problems to solve the given linear programming problem. 
(Multiple Choice)
4.8/5  (27)
(27)
Use the simplex method for solving nonstandard problems to solve the given linear programming problem.  x = __________
y = __________
P = __________
x = __________
y = __________
P = __________
(Essay)
4.9/5  (42)
(42)
Solve the linear programming problem by the simplex method. Minimize 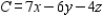 subject to
subject to 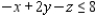
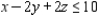

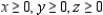
(Multiple Choice)
4.8/5  (28)
(28)
Use the simplex method for solving nonstandard problems to solve the given linear programming problem. 
(Multiple Choice)
4.8/5  (40)
(40)
Consider the linear programming problem. Maximize 
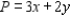 subject to
subject to 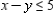
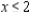
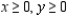 Sketch the feasible set for the linear programming problem.
Sketch the feasible set for the linear programming problem.
(Multiple Choice)
4.8/5  (39)
(39)
Check that the given simplex tableau is not in final form. Find the pivot element to be used in the next iteration of the simplex method. 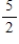
(Multiple Choice)
4.8/5  (39)
(39)
A furniture company is introducing a new line of executive desks made from a specially selected grade of walnut. Initially, three models - A, B, and C - are to be marketed. Each model A desk requires 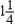 hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model B desk requires
hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model B desk requires 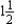 hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model C desk requires
hr for fabrication, 1 hr for assembly, and 1 hr for finishing; each model C desk requires 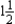 hr,
hr, 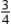 hr, and
hr, and 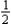 hr for fabrication, assembly, and finishing, respectively. The profit on each model A desk is $39, the profit on each model B desk is $42, and the profit on each model C desk is $31. The total time available in the fabrication department, the assembly department, and the finishing department in the first month of production is 265 hr, 176 hr, and 160 hr, respectively. To maximize company's profit, how many desks of each model should be made in the month?
__________ units of model A,
__________ units of model B,
__________ units of model C
What is the largest profit the company can realize? $ __________
Are there any resources left over?
__________ hr left over in the fabrication department,
__________ hr left over in the assembly department,
__________ hr left over in the finishing department
hr for fabrication, assembly, and finishing, respectively. The profit on each model A desk is $39, the profit on each model B desk is $42, and the profit on each model C desk is $31. The total time available in the fabrication department, the assembly department, and the finishing department in the first month of production is 265 hr, 176 hr, and 160 hr, respectively. To maximize company's profit, how many desks of each model should be made in the month?
__________ units of model A,
__________ units of model B,
__________ units of model C
What is the largest profit the company can realize? $ __________
Are there any resources left over?
__________ hr left over in the fabrication department,
__________ hr left over in the assembly department,
__________ hr left over in the finishing department
(Essay)
4.7/5  (39)
(39)
Showing 61 - 80 of 115
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)