Exam 5: Utility Game Theory
Exam 1: Introduction61 Questions
Exam 2: Introduction to Probability54 Questions
Exam 3: Probability Distributions84 Questions
Exam 4: Decision Analysis69 Questions
Exam 5: Utility Game Theory56 Questions
Exam 6: Time Series Analysis Forecasting46 Questions
Exam 7: Intro to Linear Programming49 Questions
Exam 8: LP Sensitivity Analysis59 Questions
Exam 9: LP Applications60 Questions
Exam 10: Distribution Network Models68 Questions
Exam 11: Integer Linear Programming61 Questions
Exam 12: Advanced Optimization Applications56 Questions
Exam 13: Project Scheduling58 Questions
Exam 14: Inventory Models68 Questions
Exam 15: Waiting Line Models66 Questions
Exam 16: Simulation62 Questions
Exam 17: Markov Processes41 Questions
Select questions type
Generally,the analyst must make pairwise comparisons of the decision strategies in an attempt to identify dominated strategies.
Free
(True/False)
5.0/5  (32)
(32)
Correct Answer:
True
To select a strategy in a two-person,zero-sum game,Player A follows a ______ procedure and Player B follows a ______ procedure.
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
D
For a game with an optimal pure strategy,which of the following statements is false?
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
D
When the utility function for a risk-neutral decision maker is graphed (with monetary value on the horizontal axis and utility on the vertical axis),the function appears as
(Multiple Choice)
4.9/5  (29)
(29)
Determine decision strategies based on expected value and on expected utility for this decision tree.Use the utility function
Payoff Indifference Probability 500 1.00 350 .89 300 .84 180 .60 100 .43 40 .20 20 .13 0 0 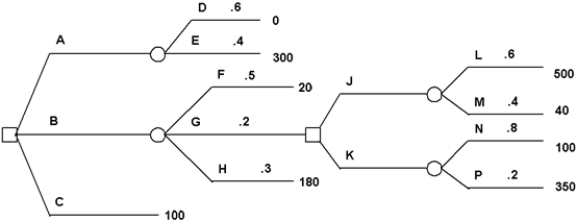
(Essay)
4.9/5  (30)
(30)
Burger Prince Restaurant is considering the purchase of a $100,000 fire insurance policy.The fire statistics indicate that in a given year the probability of property damage in a fire is as follows:
Fire Damage \ 100,000 \ 75,000 \ 50,000 \ 25,000 \ 10,000 \ 0 Probability .006 .002 .004 .003 .005 .980
a.If Burger Prince was risk neutral,how much would they be willing to pay for fire insurance?
b.If Burger Prince has the utility values given below,approximately how much would they be willing to pay for fire insurance?
Loss \ 100,000 \ 75,000 \ 50,000 \ 25,000 \ 10,000 \ 5,000 \ 0 Utility 0 30 60 85 95 99 100
(Essay)
4.9/5  (34)
(34)
A game has a pure strategy solution when both players' single-best strategies are the same.
(True/False)
4.9/5  (27)
(27)
Expected utility is a particularly useful tool when payoffs stay in a range considered reasonable by the decision maker.
(True/False)
4.7/5  (31)
(31)
A decision maker who is considered to be a risk taker is faced with this set of probabilities and payoffs
For the lottery p(80)+ (1 − p)(−50),this decision maker has assessed the following indifference probabilities
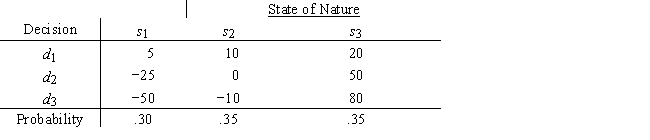 Rank the decision alternatives on the basis of expected value and on the basis of expected utility.
Payoff Probability 50 .60 20 .35 10 .25 5 .22 0 .20 -10 .18 -25 .10
Rank the decision alternatives on the basis of expected value and on the basis of expected utility.
Payoff Probability 50 .60 20 .35 10 .25 5 .22 0 .20 -10 .18 -25 .10
(Essay)
4.8/5  (31)
(31)
If a game larger than 2 X 2 requires a mixed strategy,we attempt to reduce the size of the game by
(Multiple Choice)
4.8/5  (37)
(37)
If the maximin and minimax values are not equal in a two-person zero-sum game,
(Multiple Choice)
4.9/5  (36)
(36)
Draw the utility curves for three types of decision makers,label carefully,and explain the concepts of increasing and decreasing marginal returns for money.
(Essay)
4.7/5  (32)
(32)
The decision alternative with the best expected monetary value will always be the most desirable decision.
(True/False)
4.8/5  (30)
(30)
If it is optimal for both players in a two-person,zero-sum game to select one strategy and stay with that strategy regardless of what the other player does,the game
(Multiple Choice)
4.9/5  (33)
(33)
With a mixed strategy,the optimal solution for each player is to randomly select among two or more of the alternative strategies.
(True/False)
4.7/5  (34)
(34)
To assign utilities,consider the best and worst payoffs in the entire decision situation.
(True/False)
4.8/5  (34)
(34)
The utility function for a risk avoider typically shows a diminishing marginal return for money.
(True/False)
4.8/5  (34)
(34)
A decision maker has chosen .4 as the probability for which he cannot choose between a certain loss of 10,000 and the lottery p(−25000)+ (1 − p)(5000).If the utility of −25,000 is 0 and of 5000 is 1,then the utility of −10,000 is
(Multiple Choice)
4.8/5  (42)
(42)
Showing 1 - 20 of 56
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)