Exam 10: Distribution Network Models
Explain what adjustments can be made to the transportation linear program when there are unacceptable routes.
When there are unacceptable routes in a transportation linear program, several adjustments can be made to address this issue.
1. Remove the unacceptable routes: The first and most straightforward adjustment is to simply remove the unacceptable routes from the transportation network. This may involve finding alternative routes or modes of transportation to replace the unacceptable ones.
2. Add constraints: Another approach is to add constraints to the linear program that explicitly prohibit the use of the unacceptable routes. This can be done by setting upper bounds on the flow of goods through these routes or by adding binary variables to indicate whether a route is used or not.
3. Modify costs: The costs associated with using the unacceptable routes can be adjusted to reflect their undesirability. This can be done by increasing the transportation costs for these routes or by introducing penalty costs for using them.
4. Introduce alternative routes: If possible, alternative routes that are acceptable can be introduced into the transportation network to replace the unacceptable ones. This may involve identifying new transportation providers or reconfiguring the existing network.
By making these adjustments, the transportation linear program can be modified to ensure that only acceptable routes are used for transporting goods, thereby improving the efficiency and effectiveness of the transportation network.
Define the variables and constraints necessary in the LP formulation of the transshipment problem.
The transshipment problem involves determining the optimal flow of goods from multiple sources to multiple destinations, while also allowing for intermediate transshipment points where goods can be temporarily stored and transferred. In the LP formulation of the transshipment problem, the following variables and constraints are necessary:
Variables:
1. Flow variables: These represent the amount of goods flowing from a source to a destination, or from a transshipment point to another point. These variables are typically denoted as Xij, where i represents the source or transshipment point, and j represents the destination or transshipment point.
Constraints:
1. Supply constraints: These constraints ensure that the total amount of goods leaving each source does not exceed its supply capacity.
2. Demand constraints: These constraints ensure that the total amount of goods arriving at each destination meets its demand requirements.
3. Transshipment constraints: These constraints ensure that the total amount of goods entering a transshipment point equals the total amount leaving the transshipment point, taking into account any storage or transfer capabilities at the transshipment point.
4. Non-negativity constraints: These constraints ensure that the flow variables are non-negative, as goods cannot flow in negative quantities.
By formulating the transshipment problem as an LP with these variables and constraints, it becomes possible to optimize the flow of goods while satisfying the supply, demand, and transshipment requirements.
Which of the following is not true regarding the linear programming formulation of a transportation problem?
C
The maximal flow problem can be formulated as a capacitated transshipment problem.
The network flows into and out of demand nodes are what makes the production and inventory application modeled in the textbook a
When the number of agents exceeds the number of tasks in an assignment problem,one or more dummy tasks must be introduced in the LP formulation or else the LP will not have a feasible solution.
In the LP formulation of a maximal flow problem,a conservation-of-flow constraint ensures that an arc's flow capacity is not exceeded.
The number of units shipped from origin i to destination j is represented by
The direction of flow in the shortest-route problem is always out of the origin node and into the destination node.
If a transportation problem has four origins and five destinations,the LP formulation of the problem will have
A transshipment problem is a generalization of the transportation problem in which certain nodes are neither supply nodes nor destination nodes.
When a route in a transportation problem is unacceptable,the corresponding variable can be removed from the LP formulation.
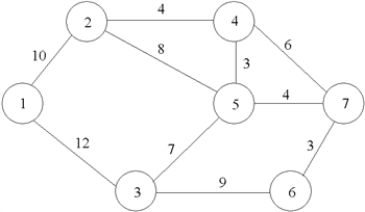
Consider the network below.Formulate the LP for finding the shortest-route path from node 1 to node 7.
A transportation problem with 3 sources and 4 destinations will have 7 decision variables.
Fodak must schedule its production of camera film for the first four months of the year.Film demand (in 1,000s of rolls)in January,February,March and April is expected to be 300,500,650 and 400,respectively.Fodak's production capacity is 500 thousand rolls of film per month.The film business is highly competitive,so Fodak cannot afford to lose sales or keep its customers waiting.Meeting month i 's demand with month i +1's production is unacceptable.
Film produced in month i can be used to meet demand in month i or can be held in inventory to meet demand in month i +1 or month i +2 (but not later due to the film's limited shelflife).There is no film in inventory at the start of January.
The film's production and delivery cost per thousand rolls will be $500 in January and February.This cost will increase to $600 in March and April due to a new labor contract.Any film put in inventory requires additional transport costing $100 per thousand rolls.It costs $50 per thousand rolls to hold film in inventory from one month to the next.
a.Modeling this problem as a transshipment problem,draw the network representation.
b.Formulate and solve this problem as a linear program.
A transshipment constraint must contain a variable for every arc entering or leaving the node.
A foreman is trying to assign crews to produce the maximum number of parts per hour of a certain product.He has three crews and four possible work centers.The estimated number of parts per hour for each crew at each work center is summarized below.Solve for the optimal assignment of crews to work centers.

The problem which deals with the distribution of goods from several sources to several destinations is the
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)