Exam 8: LP Sensitivity Analysis
Exam 1: Introduction61 Questions
Exam 2: Introduction to Probability54 Questions
Exam 3: Probability Distributions84 Questions
Exam 4: Decision Analysis69 Questions
Exam 5: Utility Game Theory56 Questions
Exam 6: Time Series Analysis Forecasting46 Questions
Exam 7: Intro to Linear Programming49 Questions
Exam 8: LP Sensitivity Analysis59 Questions
Exam 9: LP Applications60 Questions
Exam 10: Distribution Network Models68 Questions
Exam 11: Integer Linear Programming61 Questions
Exam 12: Advanced Optimization Applications56 Questions
Exam 13: Project Scheduling58 Questions
Exam 14: Inventory Models68 Questions
Exam 15: Waiting Line Models66 Questions
Exam 16: Simulation62 Questions
Exam 17: Markov Processes41 Questions
Select questions type
LINDO output is given for the following linear programming problem.
MIN 12 X1 + 10 X2 + 9 X3
SUBJECT TO
END
LP OPTIMUM FOUND AT STEP 1
OBJECTIVE FUNCTION VALUE
1)80.000000
2)
3) VARIABLE VALUE REDUCED COST 1 .000000 4.000000 2 8.000000 .000000 3 .000000 4.000000 NO.ITERATIONS= 1
RANGES IN WHICH THE BASIS IS UNCHANGED:
ROW SLACK OR SURPLUS DUAL PRICE 2) 4.000000 .000000 3) 000000 -1.000000 
 a.What is the solution to the problem?
b.Which constraints are binding?
c.Interpret the reduced cost for x1.
d.Interpret the dual price for constraint 2.
e.What would happen if the cost of x1 dropped to 10 and the cost of x2 increased to 12?
a.What is the solution to the problem?
b.Which constraints are binding?
c.Interpret the reduced cost for x1.
d.Interpret the dual price for constraint 2.
e.What would happen if the cost of x1 dropped to 10 and the cost of x2 increased to 12?
Free
(Essay)
4.9/5  (27)
(27)
Correct Answer:
a.
b. Constraint 2 is binding.
c. c1 would have to decrease by 4 or more for to become positive.
d. Increasing the right-hand side by 1 will cause a negative improvement, or increase, of 1 in this minimization objective function.
e. The sum of the percentage changes is so the solution would not change.
Use the following Management Scientist output to answer the questions.
LINEAR PROGRAMMING PROBLEM
MAX 31X1+35X2+32X3
S.T.
OPTIMAL SOLUTION
Objective Function Value = 763.333
1)
2)
3) Variable Value Reduced Cost 1 13.333 0.000 2 10.000 0.000 3 0.000 10.889 OBJECTIVE COEFFICIENT RANGES
Constraint Slack/Surplus Dual Price 1 0.000 -0.778 2 0.000 5.556 3 23.333 0.000 RIGHT HAND SIDE RANGES
Variable Lower Limit Current Value Upper Limit X1 30.000 31.000 No Upper Limit X2 No Lower Limit 35.000 36.167 X3 No Lower Limit 32.000 42.889 Constraint Lower Limit Current Value Upper Limit 1 77.647 90.000 107.143 2 126.000 150.000 163.125 3 96.667 120.000 No Upper Limit
a.Give the solution to the problem.
b.Which constraints are binding?
c.What would happen if the coefficient of x1 increased by 3?
d.What would happen if the right-hand side of constraint 1 increased by 10?
Free
(Essay)
4.9/5  (41)
(41)
Correct Answer:
a.
b. Constraints 1 and 2 are binding.
c. The value of the objective functi on would increase by 40 .
d. The value of the objective functi on would decrease by .
Any change to the objective function coefficient of a variable that is positive in the optimal solution will change the optimal solution.
Free
(True/False)
4.8/5  (28)
(28)
Correct Answer:
False
Eight of the entries have been deleted from the LINDO output that follows.Use what you know about linear programming to find values for the blanks.
MIN 6 X1 + 7.5 X2 + 10 X3
SUBJECT TO
END
LP OPTIMUM FOUND AT STEP 2
OBJECTIVE FUNCTION VALUE
2)
3) 1)612.50000
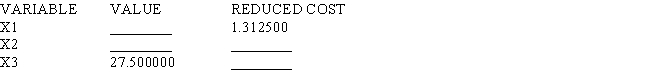 NO.ITERATIONS= 2
RANGES IN WHICH THE BASIS IS UNCHANGED:
ROW SLACK OR SURPLUS DUAL PRICE 2) -.125000 3) -.781250
NO.ITERATIONS= 2
RANGES IN WHICH THE BASIS IS UNCHANGED:
ROW SLACK OR SURPLUS DUAL PRICE 2) -.125000 3) -.781250 

(Essay)
4.8/5  (30)
(30)
In a linear programming problem,the binding constraints for the optimal solution are
5X + 3Y ≤ 30
2X + 5Y ≤ 20
a.Fill in the blanks in the following sentence:
As long as the slope of the objective function stays between _______ and _______,the current optimal solution point will remain optimal.
b.Which of these objective functions will lead to the same optimal solution?
1)2X + 1Y 2)7X + 8Y 3)80X + 60Y 4)25X + 35Y
(Essay)
4.8/5  (37)
(37)
If the range of feasibility indicates that the original amount of a resource,which was 20,can increase by 5,then the amount of the resource can increase to 25.
(True/False)
5.0/5  (47)
(47)
If the optimal value of a decision variable is zero and its reduced cost is zero,this indicates that alternative optimal solutions exist.
(True/False)
4.9/5  (35)
(35)
When the right-hand sides of two constraints are each increased by one unit,the objective function value will be adjusted by the sum of the constraints' dual prices.
(True/False)
4.8/5  (43)
(43)
The dual price associated with a constraint is the change in the value of the solution per unit decrease in the right-hand side of the constraint.
(True/False)
4.7/5  (30)
(30)
A negative dual price for a constraint in a minimization problem means
(Multiple Choice)
4.8/5  (28)
(28)
Portions of a Management Scientist output are shown below.Use what you know about the solution of linear programs to fill in the ten blanks.
LINEAR PROGRAMMING PROBLEM
MAX 12X1+9X2+7X3
S.T.
OPTIMAL SOLUTION
Objective Function Value = 336.000
1)
2)
3)
4) 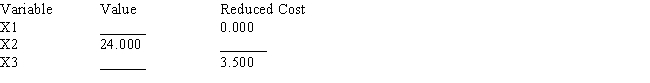 OBJECTIVE COEFFICIENT RANGES
OBJECTIVE COEFFICIENT RANGES
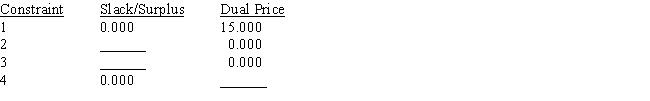 RIGHT HAND SIDE RANGES
Variable Lower Limit Current Value Upper Limit 1 5.400 12.000 No Upper Limit 2 2.000 9.000 20.000 3 No Lower Limit 7.000 10.500
RIGHT HAND SIDE RANGES
Variable Lower Limit Current Value Upper Limit 1 5.400 12.000 No Upper Limit 2 2.000 9.000 20.000 3 No Lower Limit 7.000 10.500 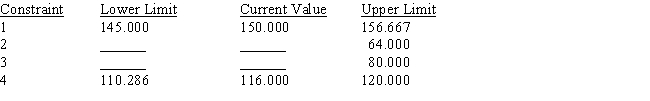
(Essay)
5.0/5  (35)
(35)
How would sensitivity analysis of a linear program be undertaken if one wishes to consider simultaneous changes for
both the right-hand-side values and objective function.
(Essay)
4.8/5  (33)
(33)
Sensitivity analysis information in computer output is based on the assumption of
(Multiple Choice)
4.8/5  (38)
(38)
For a minimization problem,a positive dual price indicates the value of the objective function will increase.
(True/False)
4.9/5  (32)
(32)
Sensitivity analysis is concerned with how certain changes affect
(Multiple Choice)
4.7/5  (40)
(40)
A section of output from The Management Scientist is shown here. What will happen if the right-hand-side for constraint 2 increases by 200?
Constraint Lower Limit Current Value Upper Limit 2 240 300 420
(Multiple Choice)
4.9/5  (35)
(35)
The optimal solution of the linear programming problem is at the intersection of constraints 1 and 2.
Max 2+ s.t. 4+1\leq400 4+3\leq600 1+2\leq300 ,\geq0
a.
Over what range can the coefficient of x1 vary before the current solution is no longer optimal?
b.
Over what range can the coefficient of x2 vary before the current solution is no longer optimal?
c.Compute the dual prices for the three constraints.
(Essay)
4.8/5  (29)
(29)
How is sensitivity analysis used in linear programming? Given an example of what type of questions that can be
answered.
(Essay)
5.0/5  (35)
(35)
An objective function reflects the relevant cost of labor hours used in production rather than treating them as a sunk cost.The correct interpretation of the dual price associated with the labor hours constraint is
(Multiple Choice)
4.8/5  (37)
(37)
Showing 1 - 20 of 59
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)