Exam 17: Markov Processes
Exam 1: Introduction61 Questions
Exam 2: Introduction to Probability54 Questions
Exam 3: Probability Distributions84 Questions
Exam 4: Decision Analysis69 Questions
Exam 5: Utility Game Theory56 Questions
Exam 6: Time Series Analysis Forecasting46 Questions
Exam 7: Intro to Linear Programming49 Questions
Exam 8: LP Sensitivity Analysis59 Questions
Exam 9: LP Applications60 Questions
Exam 10: Distribution Network Models68 Questions
Exam 11: Integer Linear Programming61 Questions
Exam 12: Advanced Optimization Applications56 Questions
Exam 13: Project Scheduling58 Questions
Exam 14: Inventory Models68 Questions
Exam 15: Waiting Line Models66 Questions
Exam 16: Simulation62 Questions
Exam 17: Markov Processes41 Questions
Select questions type
Transition probabilities are conditional probabilities.
Free
(True/False)
4.8/5  (43)
(43)
Correct Answer:
True
On any particular day an individual can take one of two routes to work.Route A has a 25% chance of being congested,whereas route B has a 40% chance of being congested.
The probability of the individual taking a particular route depends on his previous day's experience.If one day he takes route A and it is not congested,he will take route A again the next day with probability .8.If it is congested,he will take route B the next day with probability .7.
On the other hand,if on a day he takes route B and it is not congested,he will take route B again the next day with probability .9.Similarly if route B is congested,he will take route A the next day with probability .6.
a.Construct the transition matrix for this problem.(HINT: There are 4 states corresponding to the route taken and the congestion.The transition probabilities are products of the independent probabilities of congestion and next day choice. )
b.What is the long-run proportion of time that route A is taken?
Free
(Essay)
4.8/5  (38)
(38)
Correct Answer:
a/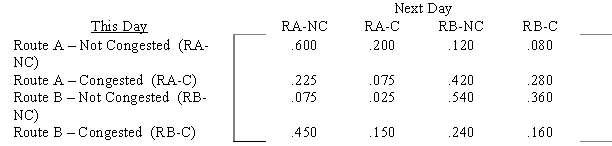
b..36 + .12 = .48
Discuss three types of information provided by analysis of a Markov process.
(Essay)
5.0/5  (35)
(35)
A recent study done by an economist for the Small Business Administration investigated failures of small business.Failures were either classified as due to poor financing,poor management,or a poor product.The failure rates differed for new businesses (under one year old)versus established businesses (over one year old. )
As the result of the economist's study,the following probabilities were determined.For new businesses the probability of failure due to financing was .15,due to management .20,and due to product .05.The corresponding probabilities for established businesses were .10,.06,and .03 respectively.
a.
Determine a five-state Markov Chain transition matrix with states for new,established,and each of the three failure states.Write it in the form of I,O,R,and Q submatrices.
b.Determine the probability that a new business will survive during the next three years.
c.What proportion of new businesses eventually fail due to:
(1)poor financing? (2)poor management? (3)poor product?
(Essay)
4.7/5  (38)
(38)
The probability that a system is in a particular state after a large number of periods is
(Multiple Choice)
4.7/5  (33)
(33)
When absorbing states are present,each row of the transition matrix corresponding to an absorbing state will have a single 1 and all other probabilities will be 0.
(True/False)
4.7/5  (40)
(40)
The probability that the system is in state 2 in the 5th period is π5(2).
(True/False)
4.8/5  (48)
(48)
For Markov processes having the memoryless property,the prior states of the system must be considered in order to predict the future behavior of the system.
(True/False)
4.9/5  (35)
(35)
The fundamental matrix is used to calculate the probability of the process moving into each absorbing state.
(True/False)
4.8/5  (36)
(36)
All entries in a row of a matrix of transition probabilities sum to 1.
(True/False)
4.7/5  (31)
(31)
The sum of the probabilities in a transition matrix equals the number of rows in the matrix.
(True/False)
4.9/5  (36)
(36)
All Markov chain transition matrices have the same number of rows as columns.
(True/False)
4.9/5  (33)
(33)
Accounts receivable have been grouped into the following states:
State 1: Paid
State 2: Bad debt
State 3: 0-30 days old
State 4: 31-60 days old
Sixty percent of all new bills are paid before they are 30 days old.The remainder of these go to state 4.Seventy percent of all 30 day old bills are paid before they become 60 days old.If not paid,they are permanently classified as bad debts.
a.Set up the one month Markov transition matrix.
b.What is the probability that an account in state 3 will be paid?
(Essay)
4.8/5  (43)
(43)
Showing 1 - 20 of 41
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)