Solved

Consider the First-Order Differential Equation

Question 77

Essay

Consider the first-order differential equation
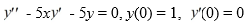Consider the first-order differential equation . Assume a solution of this equation can be represented as a power series . Write down the following explicit formulas for the coefficients C<sub>n</sub> . .
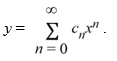Assume a solution of this equation can be represented as a power series Consider the first-order differential equation . Assume a solution of this equation can be represented as a power series . Write down the following explicit formulas for the coefficients C<sub>n</sub> . .
Write down the following explicit formulas for the coefficients Cn
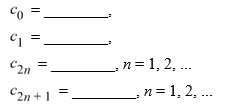Consider the first-order differential equation . Assume a solution of this equation can be represented as a power series . Write down the following explicit formulas for the coefficients C<sub>n</sub> . .

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q71: Which of these are ordinary points for

Q72: What is the greatest lower bound for

Q73: x = 0 is a regular singular

Q74: Consider the second-order differential equation <img

Q75: Consider the second-order differential equation <img

Q76: What is a lower bound for the

Q78: Consider the second-order differential equation <img

Q79: Consider the Bessel functions of the

Q80: Which of the following pairs forms

Q81: Consider the Bessel equation of order <img