Consider the Bessel Functions of the First Kind of Orders $J_{0}$

Multiple Choice

Consider the Bessel functions of the first kind of orders zero and one, respectively, given by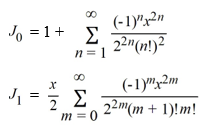
.
Which of these are properties of these functions? Select all that apply.

A) $J_{0}$ has only finitely many zeroes for $x>0$ .
B) Both series converge absolutely for all real numbers $x$ .
C) $J_{1}(x) =-J_{0}{ }^{\prime}(x)$ , for all real numbers $x$ .
D) $J_{0}(x) \rightarrow 0$ as $x \rightarrow 0^{+}$
E) $J_{0}(x) \cong\left(\frac{2}{\pi x}\right) ^{\frac{1}{2}} \cos \left(x-\frac{\pi}{4}\right)$ as $x \rightarrow \infty$
F) $J_{0}(x) \cong\left(\frac{2}{\pi x}\right) ^{\frac{1}{2}} \sin \left(x-\frac{\pi}{4}\right)$