Consider the Second-Order Differential Equation $y_{1}(x)=\sum_{n=0}^{\infty} a_{n} x^{n}, y_{2}(x)=x^{-\frac{1}{4}} \sum_{n=0}^{\infty} b_{n} x^{n}$

Multiple Choice

Consider the second-order differential equation .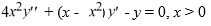
Suppose the method of Frobenius is used to determine the general solution of this differential equation.
Which of the following is the form of a pair of linearly independent solution of this differential

A) $y_{1}(x) =\sum_{n=0}^{\infty} a_{n} x^{n}, y_{2}(x) =x^{-\frac{1}{4}} \sum_{n=0}^{\infty} b_{n} x^{n}$
B) $y_{1}(x) =\sum_{n=0}^{\infty} a_{n} x^{n+1}, y_{2}(x) =x^{-\frac{1}{4}} \sum_{n=0}^{\infty} b_{n} x^{n}$
C) $y_{1}(x) =\sum_{n=0}^{\infty} a_{n} x^{n}, y_{2}(x) =x^{\frac{3}{4}} \sum_{n=0}^{\infty} b_{n} x^{n}$
D) $y_{1}(x) =\sum_{n=0}^{\infty} a_{n} x^{n+1}, y_{2}(x) =x^{\frac{3}{4}} \sum_{n=0}^{\infty} b_{n} x^{n}$
E) $y_{1}(x) =\ln (x) \sum_{n=0}^{\infty} a_{n} x^{n+1}, y_{2}(x) =x^{-\frac{1}{4}} \sum_{n=0}^{\infty} b_{n} x^{n}$