Exam 5: Uncertainty and Consumer Behavior
Exam 1: Preliminaries77 Questions
Exam 2: The Basics of Supply and Demand135 Questions
Exam 3: Consumer Behavior146 Questions
Exam 4: Individual and Market Demand173 Questions
Exam 5: Uncertainty and Consumer Behavior177 Questions
Exam 6: Production123 Questions
Exam 7: The Cost of Production166 Questions
Exam 8: Profit Maximization and Competitive Supply149 Questions
Exam 9: The Analysis of Competitive Markets177 Questions
Exam 10: Market Power: Monopoly and Monopsony158 Questions
Exam 11: Pricing With Market Power122 Questions
Exam 12: Monopolistic Competition and Oligopoly113 Questions
Exam 13: Game Theory and Competitive Strategy150 Questions
Exam 14: Markets for Factor Inputs123 Questions
Exam 15: Investment, Time, and Capital Markets153 Questions
Exam 16: General Equilibrium and Economic Efficiency111 Questions
Exam 17: Markets With Asymmetric Information130 Questions
Exam 18: Externalities and Public Goods123 Questions
Select questions type
People often use probability statements to describe events that can only happen once. For example, a political consultant may offer their opinion about the probability that a particular candidate may win the next election. Probability statements like these are based on ________ probabilities.
(Multiple Choice)
4.8/5  (39)
(39)
An individual with a constant marginal utility of income will be
(Multiple Choice)
4.9/5  (37)
(37)
Irene's utility of income function is U(I) = 20I + 300. Irene is offered the following game of chance. The odds of winning are 1/100 and the pay-off is 75 times the wager. If she loses, she loses her wager amount. Calculate Irene's expected utility of the game.
(Essay)
4.9/5  (42)
(42)
Consider the following information about job opportunities for new college graduates in Megalopolis:Table 5.1
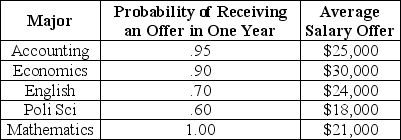 -Refer to Table 5.1. Ranked highest to lowest in expected income, the majors are
-Refer to Table 5.1. Ranked highest to lowest in expected income, the majors are
(Multiple Choice)
4.8/5  (39)
(39)
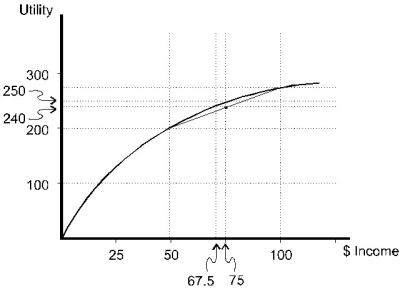 Figure 5.2
-When facing a 50% chance of receiving $50 and a 50% chance of receiving $100, the individual pictured in Figure 5.2
Figure 5.2
-When facing a 50% chance of receiving $50 and a 50% chance of receiving $100, the individual pictured in Figure 5.2
(Multiple Choice)
4.9/5  (32)
(32)
Consider the following information about job opportunities for new college graduates in Megalopolis:Table 5.1
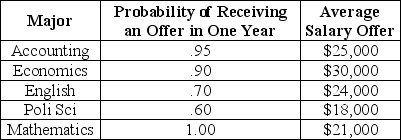 -Refer to Table 5.1. A risk-averse student making a decision solely on the basis of the above information
-Refer to Table 5.1. A risk-averse student making a decision solely on the basis of the above information
(Multiple Choice)
4.7/5  (27)
(27)
Jonathan and Roberto enjoy playing poker. Jonathan's utility as a function of winning a poker hand is UJ = { 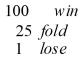 .
Roberto's utility as a function of winning a poker hand is UR = {
.
Roberto's utility as a function of winning a poker hand is UR = { 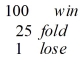 .
Unfortunately for Jonathan, he has a habit of whistling only when he gets a full-house or better. Roberto, however, has not noticed this habit. Roberto currently has three-of-a-kind (which will lose to a full-house or better). Roberto believes that the probability Jonathan can beat his three-of-a-kind is 1/10. Roberto could choose to fold or play the hand. Calculate Roberto's expected utility according to his beliefs. Jonathan is currently whistling. How much could Roberto increase his utility by recognizing Jonathan's whistling habit?
.
Unfortunately for Jonathan, he has a habit of whistling only when he gets a full-house or better. Roberto, however, has not noticed this habit. Roberto currently has three-of-a-kind (which will lose to a full-house or better). Roberto believes that the probability Jonathan can beat his three-of-a-kind is 1/10. Roberto could choose to fold or play the hand. Calculate Roberto's expected utility according to his beliefs. Jonathan is currently whistling. How much could Roberto increase his utility by recognizing Jonathan's whistling habit?
(Essay)
4.9/5  (39)
(39)
Scenario 5.7:
As president and CEO of MegaWorld industries, Natasha must decide on some very risky alternative investments. Consider the following:
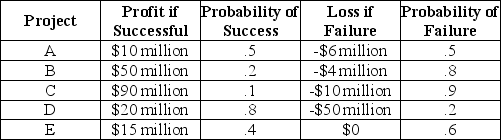 -Refer to Scenario 5.7. As a risk-neutral executive, Natasha
-Refer to Scenario 5.7. As a risk-neutral executive, Natasha
(Multiple Choice)
5.0/5  (35)
(35)
The indifference curve between expected return and the standard deviation of return for a risk-averse investor
(Multiple Choice)
4.8/5  (34)
(34)
The indifference curves of two investors are plotted against a single budget line. Indifference curve A is shown as tangent to the budget line at a point to the left of indifference curve B's tangency to the same line.
(Multiple Choice)
4.8/5  (30)
(30)
Farmer Brown grows wheat on his farm in Kansas, and the weather during the growing season makes this a risky venture. Over the many years that he has been in business, he has learned that rainfall patterns can be categorized as highly productive (HP) with a probability of .2, moderately productive (MP) with a probability of .6, and not productive at all (NP) with a probability of .2. With these various rainfall patterns, he has also learned that the inflation adjusted yields are $25,000 with NP weather, $10,000 with MP weather, and $50,000 with HP weather. Calculate the expected yield from growing wheat on Farmer Brown's farm. What can be learned about Brown's attitude toward risk from this problem? Explain.
(Essay)
4.8/5  (32)
(32)
The relationship between income and total utility for three investors (A, B, and
C) is shown in the tables below.
A B C
Income TU Income TU Income TU
5,000 14 5,000 4 5,000 6
10,000 24 10,000 8 10,000 14
15,000 32 15,000 12 15,000 24
20,000 38 20,000 16 20,000 36
25,000 43 25,000 20 25,000 52
30,000 47 30,000 24 30,000 72
35,000 49 35,000 28 35,000 100
Each investor has been confronted with the following three investment opportunities. The first opportunity is an investment which pays $15,000 risk free. Opportunity two offers a 0.4 probability of a $25,000 payment and a 0.6 probability of paying $10,000. The final investment will either pay $35,000 with a probability of 0.25 or $5,000 with a probability of 0.75. Determine the alternative each of the above investors would choose. Provide an intuitive explanation for the differences in their choices.
(Essay)
4.8/5  (39)
(39)
The tendency for individuals to assign higher values to goods when they own the goods than when they do not possess the goods is known as the:
(Multiple Choice)
4.8/5  (47)
(47)
Suppose you cannot buy information that completely removes the uncertainty from a business decision that you face, but you could buy information that reduces the degree of uncertainty. Based on the discussion in this chapter, the value of this partial information could be determined as the:
(Multiple Choice)
4.8/5  (39)
(39)
Sandra lives in the Pacific Northwest and enjoys walking to and from work during sunny days. Her utility is sharply diminished if she must walk while it is raining. Sandra's utility function is
U = 1,000 I1 + 250 I2 + 1 I3 where I2 = 1 if she walks and there is no rain and I1 = 0 otherwise, I2 = 1 if she drives to work and I2 = 0 otherwise, and I3 = 1 if she walks and it rains and I3 = 0 otherwise. Sandra believes that the probability of rain today is 3/10. Given her beliefs, what is her expected utility from walking to work? What is her expected utility from driving to work according to her beliefs? If Sandra maximizes her expected utility according to her beliefs, will she drive or walk to work? Sandra missed the weather report this morning that stated the true probability of rain today is 4/5. Given the weather report is accurate, what is Sandra's true expected utility from walking and driving to work? How much could Sandra increase her expected utility if she read and believed the weather report?
(Essay)
4.9/5  (42)
(42)
Showing 121 - 140 of 177
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)