Exam 16: Analytic Hierarchy Process
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
A pairwise comparison rating of 9 means that the two alternatives are
(Multiple Choice)
4.7/5  (37)
(37)
Upon completion of an Analytic Hierarchy Process analysis, the CR = 0.23, thus
(Multiple Choice)
4.8/5  (40)
(40)
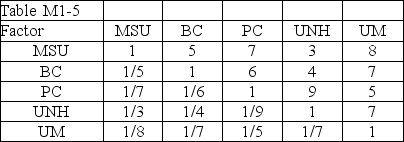
Table M1-5
It is International Day on campus and a professor of Scottish, German, and Hawaiian ancestry is weighing his options for traditional attire among his kilt, lederhosen and grass skirt.He decides to weigh these alternatives using AHP and has decided that comfort, style, and ease of use are the most important criteria.
His pairwise comparison matrices are as follows:
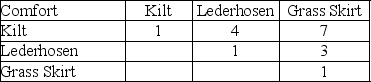
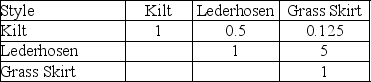
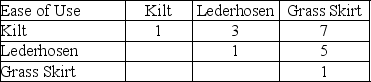
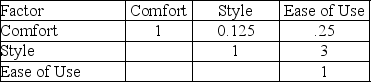 -Use Table M1-5 to determine the element in the weighted sum vector for the style factor for the lederhosen.
-Use Table M1-5 to determine the element in the weighted sum vector for the style factor for the lederhosen.
(Multiple Choice)
4.8/5  (31)
(31)
In multifactor decision making, individuals quantitatively and objectively consider the various factors in making their decisions.
(True/False)
4.9/5  (30)
(30)
Jason Rule is considering attending one of five different schools.Shown below are the priorities and the original pairwise comparison matrix. Priorities Table:
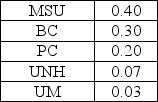 Pairwise Comparison Table:
Pairwise Comparison Table:
 The consistency vector is
The consistency vector is
(Multiple Choice)
4.9/5  (35)
(35)
Table M1-5
It is International Day on campus and a professor of Scottish, German, and Hawaiian ancestry is weighing his options for traditional attire among his kilt, lederhosen and grass skirt.He decides to weigh these alternatives using AHP and has decided that comfort, style, and ease of use are the most important criteria.
His pairwise comparison matrices are as follows:



 -Use Table M1-5 to determine the consistency ratio for the ease of use factor.
-Use Table M1-5 to determine the consistency ratio for the ease of use factor.
(Multiple Choice)
4.8/5  (34)
(34)
In AHP, if the consistency ratio demonstrates that the original pairwise comparisons are inconsistent, then the AHP evaluation should be abandoned in favor of the MFEP.
(True/False)
4.9/5  (44)
(44)
AHP gives the factor weights and factor evaluations from which the final decision can be made.
(True/False)
4.8/5  (37)
(37)
Construct an initial pairwise comparison matrix with the following information regarding an Ease of Use factor about three different commercial student information systems.System C, when compared to System A, is strongly preferred.When System C is compared to System B, System C is only moderately preferred.When compared to System A, System B is strongly preferred.
(Essay)
4.8/5  (24)
(24)
Given a consistency index of 0.2070, and an n of 5, use the following table to calculate the consistency ratio. 
(Multiple Choice)
4.8/5  (32)
(32)
Given three alternatives and their total weighted evaluation, which action should be selected? 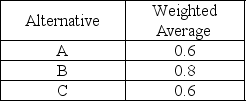
(Multiple Choice)
4.9/5  (34)
(34)
Table M1-5
It is International Day on campus and a professor of Scottish, German, and Hawaiian ancestry is weighing his options for traditional attire among his kilt, lederhosen and grass skirt.He decides to weigh these alternatives using AHP and has decided that comfort, style, and ease of use are the most important criteria.
His pairwise comparison matrices are as follows:



 -Use Table M1-5 to determine the element in the weighted sum vector for the ease of use factor for the grass skirt.
-Use Table M1-5 to determine the element in the weighted sum vector for the ease of use factor for the grass skirt.
(Multiple Choice)
4.9/5  (41)
(41)
In MFEP, the factor weights are summed and then multiplied by the total factor evaluation.
(True/False)
4.9/5  (36)
(36)
In the multifactor evaluation process, we always select the alternative that has the highest total weighted evaluation.
(True/False)
4.9/5  (29)
(29)
In AHP, the factor weights and evaluations are computed from a number of pairwise comparison matrices.
(True/False)
4.9/5  (30)
(30)
Table M1-5
It is International Day on campus and a professor of Scottish, German, and Hawaiian ancestry is weighing his options for traditional attire among his kilt, lederhosen and grass skirt.He decides to weigh these alternatives using AHP and has decided that comfort, style, and ease of use are the most important criteria.
His pairwise comparison matrices are as follows:



 -Use Table M1-5 to determine the priority for the grass skirt in the comfort factor's normalized matrix.
-Use Table M1-5 to determine the priority for the grass skirt in the comfort factor's normalized matrix.
(Multiple Choice)
4.9/5  (34)
(34)
Table M1-1
Jason Rule has developed the following table to represent his research into the decision as to which college he would like to attend after graduation:
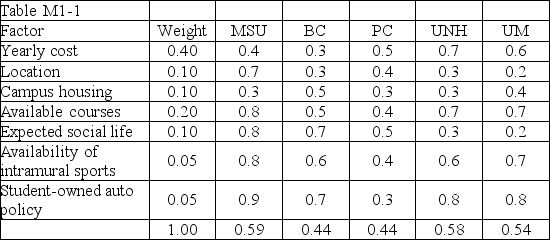 -Table M1-1 portrays Jason's initial evaluation of the colleges of interest.Jason has now decided that (a)Social Life is more important than he first implied, and (b)that the student body at MSU is so large that he may feel lost-just a small fish in a big, big pond.He decides to change the weight for Social Life to 0.2, and change his rating of the Social Life at MSU to 0.4.He will compensate for the increase in the weight of Social Life by reducing the weight of Yearly Cost.Given these changes, what will be his second-choice college?
-Table M1-1 portrays Jason's initial evaluation of the colleges of interest.Jason has now decided that (a)Social Life is more important than he first implied, and (b)that the student body at MSU is so large that he may feel lost-just a small fish in a big, big pond.He decides to change the weight for Social Life to 0.2, and change his rating of the Social Life at MSU to 0.4.He will compensate for the increase in the weight of Social Life by reducing the weight of Yearly Cost.Given these changes, what will be his second-choice college?
(Multiple Choice)
4.9/5  (37)
(37)
The consistency ratio (CR)is an indicator of the equality of factors.
(True/False)
4.9/5  (32)
(32)
Showing 41 - 60 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)