Exam 12: Waiting Lines and Queuing Theory Models
Exam 1: Introduction to Quantitative Analysis96 Questions
Exam 2: Probability Concepts and Applications155 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models129 Questions
Exam 5: Forecasting138 Questions
Exam 6: Inventory Control Models147 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods141 Questions
Exam 8: Linear Programming Applications89 Questions
Exam 9: Transportation, Assignment, and Network Models112 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming86 Questions
Exam 11: Project Management142 Questions
Exam 12: Waiting Lines and Queuing Theory Models127 Questions
Exam 13: Simulation Modeling94 Questions
Exam 14: Markov Analysis103 Questions
Exam 15: Statistical Quality Control96 Questions
Exam 16: Analytic Hierarchy Process66 Questions
Exam 17: Dynamic Programming86 Questions
Exam 18: Decision Theory and the Normal Distribution62 Questions
Exam 19: Game Theory59 Questions
Exam 20: Mathematical Tools: Determinants and Matrices104 Questions
Exam 21: Calculus-Based Optimization39 Questions
Exam 22: Linear Programming: The Simplex Method98 Questions
Exam 23: Transportation, Assignment, and Network Algorithms120 Questions
Select questions type
Little's Law concepts are applicable to all queueing models presented by the authors except the finite calling population situation.
(True/False)
4.8/5  (28)
(28)
Thanks to a generous and eccentric donor, the school of business has 3 fax machines.The toner in each machine needs to be changed after about 5 hours of use.There is one unit secretary who is responsible for the fax machine maintenance.It takes him 15 minutes to replace the toner cartridge.What is the average number of fax machines in the system?
(Multiple Choice)
4.9/5  (36)
(36)
Thanks to a generous and eccentric donor, the school of business has 3 fax machines.The toner in each machine needs to be changed after about 5 hours of use.There is one unit secretary who is responsible for the fax machine maintenance.It takes him 15 minutes to replace the toner cartridge.What is the probability that none of the fax machines need toner?
(Multiple Choice)
4.7/5  (29)
(29)
Table 12-5
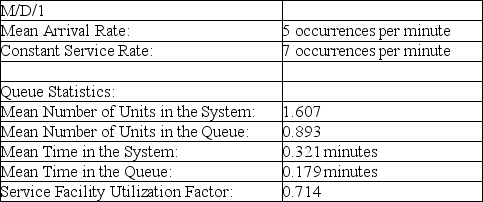 -According to the information provided in Table 12-5, which presents the solution for a queuing problem with a constant service rate, the probability that the server is idle is
-According to the information provided in Table 12-5, which presents the solution for a queuing problem with a constant service rate, the probability that the server is idle is
(Multiple Choice)
4.8/5  (36)
(36)
The school of business has 3 fax machines.The toner in each machine needs to be changed after about 5 hours of use.There is one unit secretary who is responsible for the fax machine maintenance.It takes him 15 minutes to replace the toner cartridge.What is the probability that 2 fax machines need toner at the same time?
(Multiple Choice)
4.9/5  (26)
(26)
Little's Flow Equations are applicable for single-channel systems only.
(True/False)
4.9/5  (36)
(36)
Customers arrive at their friendly DMV at a rate of 45 people per hour.There are four servers that can process customers at an average of 3 minutes.
(a)What is the average wait time?
(b)What is the average number of customers waiting?
(c)What is the average number of customers in the DMV?
(Essay)
4.8/5  (43)
(43)
Sam the Vet is running a rabies vaccination clinic for dogs at the local grade school.Sam can vaccinate a dog every 3 minutes.It is estimated that the dogs will arrive independently and randomly throughout the day at a rate of 1 dog every 6 minutes, according to a Poisson distribution.Also assume that Sam's vaccinating times are exponentially distributed.
(a)Find the probability that Sam is idle.
(b)Find the proportion of time that Sam is busy.
(c)Find the average number of dogs receiving or waiting to be vaccinated.
(d)Find the average number of dogs waiting to be vaccinated.
(e)Find the average time a dog waits before getting vaccinated.
(f)Find the average amount (mean)of time a dog spends between waiting in line and getting vaccinated.
(Essay)
4.8/5  (31)
(31)
At a local fast-food joint, cars arrive randomly at a rate of 12 every 30 minutes.The fast food joint takes an average of 2 minutes to serve each arrival.The utilization factor for this system is
(Multiple Choice)
4.9/5  (33)
(33)
Cars arrive at a parking lot entrance at the rate of 20 per hour.The average time to get a ticket and proceed to a parking space is two minutes.There are two lot attendants at the current time.The Poisson and exponential distribution appear to be relevant in this situation.
(a)What is the probability that an approaching auto must wait?
(b)What is the average waiting time?
(c)What is the average number of autos waiting to enter the garage?
(Essay)
4.7/5  (33)
(33)
A professor holds office hours during final exam week and discovers much to his dismay that his sudden popularity affords him little time to engage in his favorite activity, watching cat videos.Fifteen students per hour arrive at his office and he patiently answers questions, averaging three minutes per student.On average, how long must a student wait in line to get their last-minute questions answered?
(Multiple Choice)
4.8/5  (33)
(33)
If everything else remains constant, including the mean arrival rate and service rate, except that the service time becomes constant instead of exponential
(Multiple Choice)
4.8/5  (31)
(31)
A transient state is the normal operating condition of the queuing system.
(True/False)
4.9/5  (30)
(30)
The three major characteristics of the input source that generates arrivals or customers for the service system are
(Multiple Choice)
4.9/5  (28)
(28)
In queuing theory, the calling population is another name for
(Multiple Choice)
4.9/5  (36)
(36)
Little's Flow Equations are advantageous because if one characteristic of the operating system is known, the other characteristics can be easily found.
(True/False)
4.8/5  (33)
(33)
On a practical note-if we are using waiting line analysis to study cars passing through a single tollbooth, reneging is probably not an issue.
(True/False)
4.7/5  (36)
(36)
Showing 81 - 100 of 127
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)