Exam 13: Waiting Lines and Queuing Theory Models

At an automatic car wash, cars arrive randomly at a rate of 7 cars every 30 minutes. The car wash takes exactly 4 minutes (this is constant). On average, what would be the length of the line?

With regard to queuing theory, define what is meant by reneging.

Table 13-1 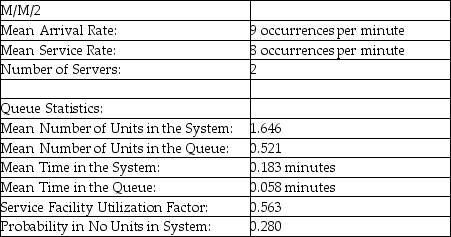-According to the information provided in Table 13-1, on average, how many units are in the line?

Table 13-1 -According to the information provided in Table 13-1, what percentage of the total available service time is being used?

Sam the Vet is running a rabies vaccination clinic for dogs at the local grade school. Sam can vaccinate a dog every 3 minutes. It is estimated that the dogs will arrive independently and randomly throughout the day at a rate of 1 dog every 4 minutes, according to a Poisson distribution. Also assume that Sam's vaccinating times are exponentially distributed. (a) Find the probability that Sam is idle. (b) Find the proportion of time that Sam is busy. (c) Find the average number of dogs receiving or waiting to be vaccinated. (d) Find the average number of dogs waiting to be vaccinated. (e) Find the average time a dog waits before getting vaccinated. (f) Find the average amount (mean) of time a dog spends between waiting in line and getting vaccinated.

With regard to queuing theory, define what is meant by balking.

Table 13-5 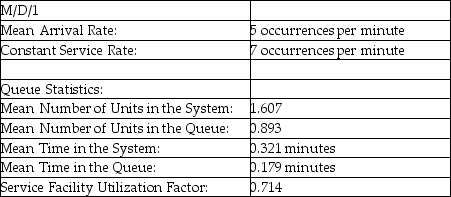-According to the information provided in Table 13-5, which presents the solution for a queuing problem with a constant service rate, what percentage of available service time is actually used?

In the multichannel model (M/M/m), we must assume that the average service time for all channels is the same.

Table 13-5 -According to the information provided in Table 13-5, which presents the solution for a queuing problem with a constant service rate, on average, how much time is spent waiting in line?

A post office has a single line for customers waiting for the next available postal clerk. There are two postal clerks who work at the same rate. The arrival rate of customers follows a Poisson distribution, while the service time follows an exponential distribution. The average arrival rate is three per minute and the average service rate is two per minute for each of the two clerks. What proportion of time are both clerks idle?

Cars arrive at a parking lot entrance at the rate of 20 per hour. The average time to get a ticket and proceed to a parking space is two minutes. There are two lot attendants at the current time. The Poisson and exponential distribution appear to be relevant in this situation. (a) What is the probability that an approaching auto must wait? (b) What is the average waiting time? (c) What is the average number of autos waiting to enter the garage?

A queue system is in a transient state before the steady state is reached.

Consider a single-server queuing system with Poisson arrivals of 10 units per hour and a constant service time of 2 minutes per unit. How long will the customer waiting time be in seconds, on average?

Table 13-5 -According to the information provided in Table 13-5, which presents the solution for a queuing problem with a constant service rate, the probability that the server is idle is ________.

Which of the following is not an assumption in common queuing mathematical models?

The school of business has 3 fax machines. The toner in each machine needs to be changed after about 5 hours of use. There is one unit secretary who is responsible for the fax machine maintenance. It takes him 15 minutes to replace the toner cartridge. What is the average waiting time in the queue?

At a local fast food joint, cars arrive randomly at a rate of 12 every 30 minutes. Service times are random (exponential) and average 2 minutes per arrival. The average time in the queue for each arrival is

Queuing theory had its beginning in the research work of ________.

A new shopping mall is considering setting up an information desk manned by one employee. Based upon information obtained from similar information desks, it is believed that people will arrive at the desk at the rate of 15 per hour. It takes exactly two minutes to answer each question. It is assumed that arrivals are Poisson. (a) Find the probability that the employee is idle. (b) Find the proportion of time that the employee is busy. (c) Find the average number of people receiving and waiting to receive information. (d) Find the average number of people waiting in line to get information. (e) Find the average time a person seeking information spends at the desk. (f) Find the expected time a person spends waiting in line to have his question answered.

Customers enter the waiting line to pay for food as they leave a cafeteria on a first-come, first-served basis. The arrival rate follows a Poisson distribution, while service times follow an exponential distribution. If the average number of arrivals is four per minute and the average service rate of a single server is seven per minute, what proportion of the time is the server busy?