Question 1

Using linear programming to maximize audience exposure in an advertising campaign is an example of the type of linear programming application known as

Accepted Answer

A)  media selection. 
B)  marketing research. 
C)  portfolio assessment. 
D)  media budgeting. 
E)  All of the above 
A)  media selection. 
B)  marketing research. 
C)  portfolio assessment. 
D)  media budgeting. 
E)  All of the above A

Question 2

Describe the marketing research linear programming application.

Accepted Answer

a decision aid for pollsters to make strategic decisions regarding survey coverage

Question 3

Table 8-1
A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 3 hours of assembly, 2 hours of finishing, and 1 hour of inspection. Each chair requires 2 hours of assembly, 2 hours of finishing, and 1 hour of inspection. The profit per table is $120 while the profit per chair is $80. Currently, each week there are 200 hours of assembly time available, 180 hours of finishing time, and 40 hours of inspection time. Linear programming is to be used to develop a production schedule. Define the variables as follows: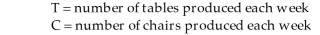  
-According to Table 8-1, which describes a production problem, suppose it is decided that the number of hours used in the assembly process must be at least 90 percent of the number of hours used in the finishing department. How would this constraint be written?

Accepted Answer

A)  3T + 2C ≥ 162 
B)  3T + 2C ≥ 0.9(2T + 2
C)  
C)  3T + 2C ≤ 162 
D)  3T + 2C ≤ 0.9(2T + 2
C)  
E)  None of the above 
A)  3T + 2C ≥ 162 
B)  3T + 2C ≥ 0.9(2T + 2
C)  
C)  3T + 2C ≤ 162 
D)  3T + 2C ≤ 0.9(2T + 2
C)  
E)  None of the above B

Question 4

Table 8-2
A small furniture manufacturer produces tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 4 hours of assembly, 3 hours of finishing, and 1 hour of inspection. Each chair requires 3 hours of assembly, 2 hours of finishing, and 2 hours of inspection. The selling price per table is $140 while the selling price per chair is $90. Currently, each week there are 220 hours of assembly time available, 160 hours of finishing time, and 45 hours of inspection time. Assume that one hour of assembly time costs $5.00; one hour of finishing time costs $6.00; one hour of inspection time costs $4.50; and that whatever labor hours are not required for the table and chairs can be applied to another product. Linear programming is to be used to develop a production schedule. Define the variables as follows: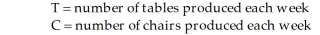  
-According to Table 8-2, which describes a production problem, what would the objective function be?

Accepted Answer

A)  Maximize T + C 
B)  Maximize 140T + 90C 
C)  Minimize 42.5T + 36C 
D)  Maximize 97.5T + 54C 
E)  Maximize 124.5T + 74.5C 
A)  Maximize T + C 
B)  Maximize 140T + 90C 
C)  Minimize 42.5T + 36C 
D)  Maximize 97.5T + 54C 
E)  Maximize 124.5T + 74.5C

Question 5

Describe a diet problem linear programming application.

Accepted Answer

a decision aid to he

Question 6

Another name for the transportation problem is the logistics problem.

Accepted Answer

A) True 
 B)False

Question 7

Ivana Miracle wishes to invest her full inheritance of $300,000, and her goal is to minimize her risk subject to an expected annual return of at least $30,000. She has decided to invest her money in any of three possible ways-CDs, which pay a guaranteed 6 percent; stocks, which have an expected return of 15 percent; and a money market mutual fund, which is expected to return 8 percent. Risk factors are 1.0 for the CDs, 3.6 for the stocks, and 1.8 for the money market fund. Formulate this as a linear program.

Accepted Answer

Let C = dollars invested in CD

Question 8

What is another name for blending problems?

Accepted Answer

A)  diet problems 
B)  ingredient problems 
C)  feed mix problems 
D)  production mix problems 
E)  media selection problems 
A)  diet problems 
B)  ingredient problems 
C)  feed mix problems 
D)  production mix problems 
E)  media selection problems

Question 9

Swearingen and McDonald, a small furniture manufacturer, produces fine hardwood tables and chairs. Each product must go through three stages of the manufacturing process: assembly, finishing, and inspection. Each table requires 12 hours of assembly, 20 hours of finishing, and 2 hours of inspection. Each chair requires 4 hours of assembly, 16 hours of finishing, and 3 hours of inspection. The profit per table is $150 while the profit per chair is $100. Currently, each week there are 300 hours of assembly time available, 220 hours of finishing time, and 30 hours of inspection time. To keep a balance, the number of chairs produced should be at least twice the number of tables. Also, the number of chairs cannot exceed 6 times the number of tables. Formulate this as a linear programming problem. Carefully define all decision variables. Find the solution.

Accepted Answer

Solution: T = 3.75,

Question 10

Table 8-5
Ivana Myrocle wishes to invest her inheritance of $200,000 so that her return on investment is maximized, but she also wishes to keep her risk level relatively low. She has decided to invest her money in any of three possible ways: CDs, which pay a guaranteed 6 percent; stocks, which have an expected return of 13 percent; and a money market mutual fund, which is expected to return 8 percent. She has decided that any or all of the $200,000 may be invested, but any part (or all) of it may be put in any of the 3 alternatives. Thus, she may have some money invested in all three alternatives. In formulating this as a linear programming problem, define the variables as follows: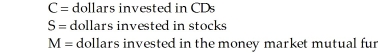  
-According to Table 8-5, which describes an investment problem, which of the following would be the most appropriate constraint in the linear programming problem?

Accepted Answer

A)  0.06C + 0.13S + 0.08M ≤ 200000 
B)  C + S + M ≥ 200000 
C)  C + S + M ≤ 200000 
D)  C + S + M = 200000 
E)  None of the above 
A)  0.06C + 0.13S + 0.08M ≤ 200000 
B)  C + S + M ≥ 200000 
C)  C + S + M ≤ 200000 
D)  C + S + M = 200000 
E)  None of the above

Question 11

Describe the portfolio selection linear programming application.

Accepted Answer

a decision aid to effectively

Question 12

Table 8-4
The following is a linear programming formulation of a labor planning problem. There are four overlapping shifts, and management must decide how many employees to schedule to start work on each shift. The objective is to minimize the total number of employees required while the constraints stipulate how many employees are required at each time of day. The variables XS1U1B11S1U1B0 - XS1U1B14S1U1B0 represent the number of employees starting work on each shift (shift 1 through shift 4).  
-According to Table 8-4, which describes a labor planning problem and its solution, how many workers would be assigned to shift 1?

Accepted Answer

A)  12 
B)  13 
C)  0 
D)  2 
E)  None of the above 
A)  12 
B)  13 
C)  0 
D)  2 
E)  None of the above

Question 13

Table 8-3
Each coffee table produced by Timothy Kent Designers nets the firm a profit of $9. Each bookcase yields a $12 profit. Kent's firm is small and its resources limited. During any given production period (of 1 week), 10 gallons of varnish and 12 lengths of high quality redwood are available. Each coffee table requires approximately 1 gallon of varnish and 1 length of redwood. Each bookcase takes 1 gallon of varnish and 2 lengths of wood.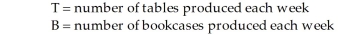  
-Referring to Table 8-3, which of the following constraints would be used?

Accepted Answer

A)  10T + 12B ≤ 12 
B)  1T + 1B ≤ 10 
C)  1T + 2B ≥ 12 
D)  All of the above 
E)  None of the above 
A)  10T + 12B ≤ 12 
B)  1T + 1B ≤ 10 
C)  1T + 2B ≥ 12 
D)  All of the above 
E)  None of the above

Question 14

Table 8-3
Each coffee table produced by Timothy Kent Designers nets the firm a profit of $9. Each bookcase yields a $12 profit. Kent's firm is small and its resources limited. During any given production period (of 1 week), 10 gallons of varnish and 12 lengths of high quality redwood are available. Each coffee table requires approximately 1 gallon of varnish and 1 length of redwood. Each bookcase takes 1 gallon of varnish and 2 lengths of wood.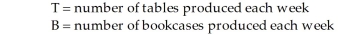  
-Referring to Table 8-3, if we were to frame this as a linear programming problem, the objective function would be:

Accepted Answer

A)  Maximize 9B + 12T. 
B)  Maximize 9T + 12B. 
C)  Minimize 10T + 10B. 
D)  Maximize 12T + 10B. 
E)  None of the above 
A)  Maximize 9B + 12T. 
B)  Maximize 9T + 12B. 
C)  Minimize 10T + 10B. 
D)  Maximize 12T + 10B. 
E)  None of the above

Question 15

The linear programming model of the production scheduling process is usually used when we have to schedule the production of a single product, requiring a mix of resources, over time.

Accepted Answer

A) True 
 B)False

Question 16

Table 8-3
Each coffee table produced by Timothy Kent Designers nets the firm a profit of $9. Each bookcase yields a $12 profit. Kent's firm is small and its resources limited. During any given production period (of 1 week), 10 gallons of varnish and 12 lengths of high quality redwood are available. Each coffee table requires approximately 1 gallon of varnish and 1 length of redwood. Each bookcase takes 1 gallon of varnish and 2 lengths of wood.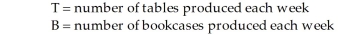  
-Referring to Table 8-3, suppose that this problem requires that you use all the varnish for the week. How would the linear programming representation change?

Accepted Answer

A)  1B + 1T ≤ 10 will become 1B + 1T ≤ 12. 
B)  1B + 1T ≤ 10 will be replaced by 1B + 1T ≥ 10. 
C)  1B + 1T ≤ 10 will become 1B + 1T = 10. 
D)  2B + 1T ≤ 12 will become 2B + 1T = 12. 
E)  None of the above 
A)  1B + 1T ≤ 10 will become 1B + 1T ≤ 12. 
B)  1B + 1T ≤ 10 will be replaced by 1B + 1T ≥ 10. 
C)  1B + 1T ≤ 10 will become 1B + 1T = 10. 
D)  2B + 1T ≤ 12 will become 2B + 1T = 12. 
E)  None of the above

Question 17

In production scheduling LP problems, inventory at the end of this month is set equal to ________.

Accepted Answer

A)  inventory at the end of last month + this month's production − this month's sales 
B)  inventory at the beginning of last month + this month's production − this month's sales 
C)  inventory at the end of last month + last month's production − this month's sales 
D)  inventory at the beginning of last month + last month's production − last month's sales 
E)  inventory at the end of last month - this month's production + this month's sales 
A)  inventory at the end of last month + this month's production − this month's sales 
B)  inventory at the beginning of last month + this month's production − this month's sales 
C)  inventory at the end of last month + last month's production − this month's sales 
D)  inventory at the beginning of last month + last month's production − last month's sales 
E)  inventory at the end of last month - this month's production + this month's sales

Question 18

Suppose that the problem described in Table 8-2 is modified to specify that one-third of the tables produced must have 6 chairs, one-third must have 4 chairs, and one-third must have 2 chairs. How would this constraint be written?

Accepted Answer

A)  C = 4T 
B)  C = 2T 
C)  C = 3T 
D)  C = 6T 
E)  None of the above 
A)  C = 4T 
B)  C = 2T 
C)  C = 3T 
D)  C = 6T 
E)  None of the above

Question 19

Media selection problems can be approached with LP from which two perspectives?

Accepted Answer

The objective can be

Question 20

When applying linear programming to diet problems, the objective function is usually designed to

Accepted Answer

A)  maximize profits from blends of nutrients. 
B)  maximize ingredient blends. 
C)  minimize production losses. 
D)  maximize the number of products to be produced. 
E)  minimize the costs of nutrient blends. 
A)  maximize profits from blends of nutrients. 
B)  maximize ingredient blends. 
C)  minimize production losses. 
D)  maximize the number of products to be produced. 
E)  minimize the costs of nutrient blends.

Using linear programming to maximize audience exposure in an advertising campaign is an example of the type of linear programming application known as

Describe the marketing research linear programming application.

Describe a diet problem linear programming application.

Another name for the transportation problem is the logistics problem.

What is another name for blending problems?

Describe the portfolio selection linear programming application.

The linear programming model of the production scheduling process is usually used when we have to schedule the production of a single product, requiring a mix of resources, over time.

In production scheduling LP problems, inventory at the end of this month is set equal to ________.

Suppose that the problem described in Table 8-2 is modified to specify that one-third of the tables produced must have 6 chairs, one-third must have 4 chairs, and one-third must have 2 chairs. How would this constraint be written?

Media selection problems can be approached with LP from which two perspectives?

When applying linear programming to diet problems, the objective function is usually designed to

Introduction to Quantitative Analysis

Probability Concepts and Applications

Decision Analysis

Regression Models

Forecasting

Inventory Control Models

Linear Programming Models: Graphical and Computer Methods

Transportation and Assignment Models

Integer Programming, Goal Programming, and Nonlinear Programming

Network Models

Project Management

Waiting Lines and Queuing Theory Models

Simulation Modeling

Markov Analysis

Statistical Quality Control

Filters

Exam 8: Linear Programming Applications

Using linear programming to maximize audience exposure in an advertising campaign is an example of the type of linear programming application known as

Describe the marketing research linear programming application.

Describe a diet problem linear programming application.

Another name for the transportation problem is the logistics problem.

What is another name for blending problems?

Describe the portfolio selection linear programming application.

The linear programming model of the production scheduling process is usually used when we have to schedule the production of a single product, requiring a mix of resources, over time.

In production scheduling LP problems, inventory at the end of this month is set equal to ________.

Suppose that the problem described in Table 8-2 is modified to specify that one-third of the tables produced must have 6 chairs, one-third must have 4 chairs, and one-third must have 2 chairs. How would this constraint be written?

Media selection problems can be approached with LP from which two perspectives?

When applying linear programming to diet problems, the objective function is usually designed to

Introduction to Quantitative Analysis

Probability Concepts and Applications

Decision Analysis

Regression Models

Forecasting

Inventory Control Models

Linear Programming Models: Graphical and Computer Methods

Transportation and Assignment Models

Integer Programming, Goal Programming, and Nonlinear Programming

Network Models

Project Management

Waiting Lines and Queuing Theory Models

Simulation Modeling

Markov Analysis

Statistical Quality Control

Filters