Exam 7: Linear Programming Models: Graphical and Computer Methods
Exam 1: Introduction to Quantitative Analysis63 Questions
Exam 2: Probability Concepts and Applications145 Questions
Exam 3: Decision Analysis119 Questions
Exam 4: Regression Models120 Questions
Exam 5: Forecasting101 Questions
Exam 6: Inventory Control Models113 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods100 Questions
Exam 8: Linear Programming Applications96 Questions
Exam 9: Transportation and Assignment Models80 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming88 Questions
Exam 11: Network Models86 Questions
Exam 12: Project Management123 Questions
Exam 13: Waiting Lines and Queuing Theory Models133 Questions
Exam 14: Simulation Modeling68 Questions
Exam 15: Markov Analysis78 Questions
Exam 16: Statistical Quality Control87 Questions
Select questions type
The Fido Dog Food Company wishes to introduce a new brand of dog biscuits (composed of chicken and liver-flavored biscuits) that meets certain nutritional requirements. The liver-flavored biscuits contain 1 unit of nutrient A and 2 units of nutrient B, while the chicken-flavored ones contain 1 unit of nutrient A and 4 units of nutrient B. According to federal requirements, there must be at least 40 units of nutrient A and 60 units of nutrient B in a package of the new biscuit mix. In addition, the company has decided that there can be no more than 15 liver-flavored biscuits in a package. If it costs 1 cent to make a liver-flavored biscuit and 2 cents to make a chicken-flavored one, what is the optimal product mix for a package of the biscuits in order to minimize the firm's cost?
(a) Formulate this as a linear programming problem.
(b) Find the optimal solution for this problem graphically.
(c) Are any constraints redundant? If so, which one or ones?
(d) What is the total cost of a package of dog biscuits using the optimal mix?
Free
(Essay)
4.9/5  (35)
(35)
Correct Answer:
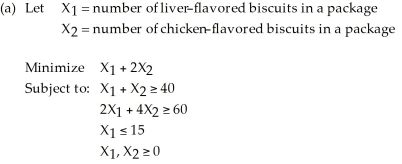 (b) Corner points (0,40) and (15,25)
(b) Corner points (0,40) and (15,25)
Optimal solution is (15,25) with cost of 65.
(c) 2X1 + 4X2 ≥ 60 is redundant.
(d) minimum cost = 65 cents
Sensitivity analyses are used to examine the effects of changes in
Free
(Multiple Choice)
5.0/5  (39)
(39)
Correct Answer:
D
Consider the following linear programming problem: 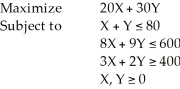 This is a special case of a linear programming problem in which
This is a special case of a linear programming problem in which
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
A
Billy Penny is trying to determine how many units of two types of lawn mowers to produce each day. One of these is the Standard model, while the other is the Deluxe model. The profit per unit on the Standard model is $60, while the profit per unit on the Deluxe model is $40. The Standard model requires 20 minutes of assembly time, while the Deluxe model requires 35 minutes of assembly time. The Standard model requires 10 minutes of inspection time, while the Deluxe model requires 15 minutes of inspection time. The company must fill an order for 6 Deluxe models. There are 450 minutes of assembly time and 180 minutes of inspection time available each day. How many units of each product should be manufactured to maximize profits?
(Essay)
4.7/5  (39)
(39)
Determine where the following two constraints intersect.
5X + 23Y ≤ 1000
10X + 26Y ≤ 1600
(Short Answer)
4.7/5  (36)
(36)
If the isoprofit line is not parallel to a constraint, then the solution must be unique.
(True/False)
4.9/5  (36)
(36)
In order for a linear programming problem to have multiple solutions, the solution must exist
(Multiple Choice)
4.8/5  (35)
(35)
When a constraint line bounding a feasible region has the same slope as an isoprofit line,
(Multiple Choice)
4.9/5  (33)
(33)
Consider the following linear programming problem: 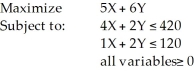 Which of the following points (X,Y) is in the feasible region?
Which of the following points (X,Y) is in the feasible region?
(Multiple Choice)
4.9/5  (35)
(35)
Consider the following linear programming problem: 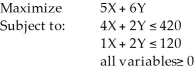 Which of the following points (X,Y) is not a feasible corner point?
Which of the following points (X,Y) is not a feasible corner point?
(Multiple Choice)
4.8/5  (36)
(36)
A plastic parts supplier produces two types of plastic parts used for electronics. Type 1 requires 30 minutes of labor and 45 minutes of machine time. Type 2 requires 60 minutes of machine hours and 75 minutes of labor. There are 600 hours available per week of labor and 800 machine hours available. The demand for custom molds and plastic parts are identical. Type 1 has a profit margin of $25 a unit and Type 2 have a profit margin of $45 a unit. The plastic parts supplier must choose the quantity of Product A and Product B to produce which maximizes profit.
(a) Formulate this as a linear programming problem.
(b) Find the solution that gives the maximum profit using either QM for Windows or Excel.
(Essay)
4.8/5  (38)
(38)
Two advertising media are being considered for promotion of a product. Radio ads cost $400 each, while newspaper ads cost $600 each. The total budget is $7,200 per week. The total number of ads should be at least 15, with at least 2 of each type. Each newspaper ad reaches 6,000 people, while each radio ad reaches 2,000 people. The company wishes to reach as many people as possible while meeting all the constraints stated. How many ads of each type should be placed?
(Essay)
4.7/5  (32)
(32)
The rationality assumption implies that solutions need not be in whole numbers (integers).
(True/False)
4.7/5  (38)
(38)
A company can decide how many additional labor hours to acquire for a given week. Subcontractor workers will only work a maximum of 20 hours a week. The company must produce at least 200 units of product A, 300 units of product B, and 400 units of product C. In 1 hour of work, worker 1 can produce 15 units of product A, 10 units of product B, and 30 units of product C. Worker 2 can produce 5 units of product A, 20 units of product B, and 35 units of product C. Worker 3 can produce 20 units of product A, 15 units of product B, and 25 units of product C. Worker 1 demands a salary of $50/hr, worker 2 demands a salary of $40/hr, and worker 3 demands a salary of $45/hr. The company must choose how many hours they should contract with each worker to meet their production requirements and minimize labor cost.
(a) Formulate this as a linear programming problem.
(b) Find the optimal solution.
(Essay)
4.7/5  (34)
(34)
Two models of a product - Regular (X) and Deluxe (Y) - are produced by a company. A linear programming model is used to determine the production schedule. The formulation is as follows: 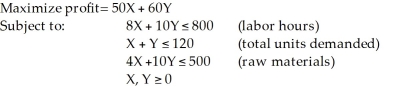 The optimal solution is X=100, Y=0. Which of these constraints is redundant?
The optimal solution is X=100, Y=0. Which of these constraints is redundant?
(Multiple Choice)
4.8/5  (36)
(36)
In a maximization problem, when one or more of the solution variables and the profit can be made infinitely large without violating any constraints, the linear program has
(Multiple Choice)
4.7/5  (45)
(45)
Showing 1 - 20 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)