Exam 15: Markov Analysis
Exam 1: Introduction to Quantitative Analysis63 Questions
Exam 2: Probability Concepts and Applications145 Questions
Exam 3: Decision Analysis119 Questions
Exam 4: Regression Models120 Questions
Exam 5: Forecasting101 Questions
Exam 6: Inventory Control Models113 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods100 Questions
Exam 8: Linear Programming Applications96 Questions
Exam 9: Transportation and Assignment Models80 Questions
Exam 10: Integer Programming, Goal Programming, and Nonlinear Programming88 Questions
Exam 11: Network Models86 Questions
Exam 12: Project Management123 Questions
Exam 13: Waiting Lines and Queuing Theory Models133 Questions
Exam 14: Simulation Modeling68 Questions
Exam 15: Markov Analysis78 Questions
Exam 16: Statistical Quality Control87 Questions
Select questions type
One of the problems with using the Markov model to study population shifts is that we must assume that the reasons for moving from one state to another remain the same over time.
Free
(True/False)
4.7/5  (32)
(32)
Correct Answer:
True
Table 15-2
The following data consists of a matrix of transition probabilities (P) of three competing retailers, the initial market share π(0). Assume that each state represents a retailer (Retailer 1, Retailer 2, Retailer 3, respectively) and the transition probabilities represent changes from one month to the next.
P =  π(0) = (0.3, 0.6, 0.1)
-Using the data given in Table 15-2, find the market shares for the three retailers in month 1.
π(0) = (0.3, 0.6, 0.1)
-Using the data given in Table 15-2, find the market shares for the three retailers in month 1.
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
B
The weather is becoming important to you since you would like to go on a picnic today. If it was sunny yesterday, there is a 65% chance it will be sunny today. If it was raining yesterday, there is a 30% chance it will be sunny today. If the probability that it was raining yesterday is 0.4, what is the probability that it will be sunny today?
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
C
Describe the situation of the existence of an equilibrium condition in a Markov analysis.
(Essay)
4.8/5  (35)
(35)
Three fast food hamburger restaurants are competing for the college lunch crowd. Burger Bills has 40% of the market while Hungry Heifer and Salty Sams each have 30% of the market. Burger Bills loses 10 % of its customers to Hungry Heifer and 10% to Salty Sams each month. Hungry Heifer loses 5% of its customers to Burger Bills and 10% to Salty Sams each month. Salty Sams loses 10% of its customers to Burger Bills while 20% go to Hungry Heifer. What will the market shares be for the three businesses next month?
(Essay)
4.8/5  (37)
(37)
Given the following matrix of transition probabilities, find the equilibrium states. 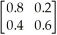
(Short Answer)
4.7/5  (36)
(36)
The copy machine in an office is very unreliable. If it was working yesterday, there is an 80% chance it will work today. If it was not working yesterday, there is a 10% chance it will work today. If it is working today, what is the probability that it will be working 2 days from now?
(Multiple Choice)
4.7/5  (33)
(33)
In the matrix of transition probabilities, Pij is the conditional probability of being in state i in the future, given the current state j.
(True/False)
4.8/5  (30)
(30)
There is a 60% chance that customer without a smart phone will buy one this year. There is a 95% chance that a customer with a smart phone will continue with a smart phone going into the next year. If 30% of target market currently own smart phones, what proportion of the target market is expected to own a smart phone next year?
(Short Answer)
4.9/5  (40)
(40)
The matrix that is needed to compute equilibrium conditions when absorbing states are involved is called a(n)
(Multiple Choice)
4.8/5  (39)
(39)
An equilibrium condition exists if the state probabilities for a future period are the same as the state probabilities for a previous period.
(True/False)
4.8/5  (29)
(29)
Markov analysis is a technique that deals with the probabilities of future occurrences by analyzing currently known probabilities.
(True/False)
4.9/5  (36)
(36)
A state probability when equilibrium has been reached is called
(Multiple Choice)
4.9/5  (38)
(38)
In a(n) ________ state, you cannot go to another state in the future.
(Multiple Choice)
4.8/5  (39)
(39)
Table 15-1
The following data consists of a matrix of transition probabilities (P) of three competing companies, and the initial market share π(0). Assume that each state represents a company (Company 1, Company 2, Company 3, respectively) and the transition probabilities represent changes from one month to the next.
P =  π(0) = (0.3, 0.6, 0.1)
-Using the data in Table 15-1, determine Company 1's estimated market share in the next period.
π(0) = (0.3, 0.6, 0.1)
-Using the data in Table 15-1, determine Company 1's estimated market share in the next period.
(Multiple Choice)
4.7/5  (34)
(34)
If in an absorbing state, the probability of being in an absorbing state in the future is ________.
(Multiple Choice)
4.9/5  (35)
(35)
Which of the following is not an assumption of Markov processes?
(Multiple Choice)
4.8/5  (49)
(49)
In Markov analysis, initial-state probability values determine equilibrium conditions.
(True/False)
4.9/5  (30)
(30)
If we want to use Markov analysis to study market shares for competitive businesses,
(Multiple Choice)
4.9/5  (34)
(34)
Showing 1 - 20 of 78
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)