Exam 14: Markov Analysis
Exam 1: Introduction to Quantitative Analysis71 Questions
Exam 2: Probability Concepts and Applications157 Questions
Exam 3: Decision Analysis128 Questions
Exam 4: Regression Models133 Questions
Exam 5: Forecasting111 Questions
Exam 6: Inventory Control Models123 Questions
Exam 7: Linear Programming Models: Graphical and Computer Methods110 Questions
Exam 8: Linear Programming Applications105 Questions
Exam 9: Transportation,assignment,and Network Models98 Questions
Exam 10: Integer Programming,goal Programming,and Nonlinear Programming98 Questions
Exam 11: Project Management134 Questions
Exam 12: Waiting Lines and Queuing Theory Models145 Questions
Exam 13: Simulation Modeling79 Questions
Exam 14: Markov Analysis86 Questions
Exam 15: Statistical Quality Control98 Questions
Exam 16: Analytic Hierarchy Process53 Questions
Exam 17: Dynamic Programming67 Questions
Exam 18: Decision Theory and the Normal Distribution50 Questions
Exam 19: Game Theory47 Questions
Exam 20: Mathematical Tools: Determinants and Matrices99 Questions
Exam 21: Calculus-Based Optimization24 Questions
Exam 22: Linear Programming: The Simplex Method100 Questions
Exam 23: Transportation, Assignment, and Network Algorithms111 Questions
Select questions type
Describe the situation of the existence of an equilibrium condition in a Markov analysis.
(Essay)
4.8/5  (35)
(35)
The matrix of transition probabilities gives the conditional probabilities of moving from one state to another.
(True/False)
4.9/5  (40)
(40)
Table 14-1
The following data consists of a matrix of transition probabilities (P)of three competing companies,and the initial market share π(0).Assume that each state represents a company (Company 1,Company 2,Company 3,respectively)and the transition probabilities represent changes from one month to the next.
P =  π(0)= (0.3,0.6,0.1)
-Using the data in Table 14-1,determine Company 2's estimated market share in the next period.
π(0)= (0.3,0.6,0.1)
-Using the data in Table 14-1,determine Company 2's estimated market share in the next period.
(Multiple Choice)
4.8/5  (43)
(43)
In Markov analysis,the likelihood that any system will change from one period to the next is revealed by the
(Multiple Choice)
4.7/5  (37)
(37)
Equilibrium state probabilities may be estimated by using Markov analysis for a large number of periods.
(True/False)
4.8/5  (38)
(38)
A certain firm has noticed that employees' salaries from year to year can be modeled by Markov analysis.The matrix of transition probabilities follows. 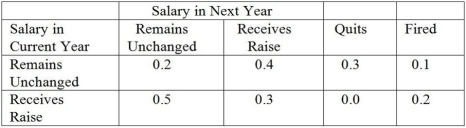 (a)Set up the matrix of transition probabilities in the form:
(a)Set up the matrix of transition probabilities in the form: 
 (b)Determine the fundamental matrix for this problem.
(c)What is the probability that an employee who has received a raise will eventually quit?
(d)What is the probability that an employee who has received a raise will eventually be fired?
(b)Determine the fundamental matrix for this problem.
(c)What is the probability that an employee who has received a raise will eventually quit?
(d)What is the probability that an employee who has received a raise will eventually be fired?
(Essay)
4.7/5  (42)
(42)
There is a 60% chance that a customer without a smart phone will buy one this year.There is a 95% chance that a customer with a smart phone will continue with a smart phone going into the next year.If 30% of target market currently own smart phones,what proportion of the target market is expected to own a smart phone next year?
(Essay)
4.9/5  (36)
(36)
In Markov analysis,the transition probability Pij represents the conditional probability of being in state i in the future given the current state of j.
(True/False)
4.7/5  (42)
(42)
Table 14-3
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P = ![Table 14-3 The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees. A B C P = π(0)= [1000,1000,1000] <sub> </sub><sub> </sub> -Using the data given in Table 14-3,what is the long run number of employees expected in location C?](https://storage.examlex.com/TB2950/11eabb83_5a40_619b_b8db_d18cdc104bec_TB2950_11_TB2950_11_TB2950_11_TB2950_11_TB2950_11.jpg)
![Table 14-3 The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees. A B C P = π(0)= [1000,1000,1000] <sub> </sub><sub> </sub> -Using the data given in Table 14-3,what is the long run number of employees expected in location C?](https://storage.examlex.com/TB2950/11eabb83_5a40_88ac_b8db_cb9f435fda4b_TB2950_11_TB2950_11_TB2950_11_TB2950_11_TB2950_11.jpg) π(0)= [1000,1000,1000]
-Using the data given in Table 14-3,what is the long run number of employees expected in location C?
π(0)= [1000,1000,1000]
-Using the data given in Table 14-3,what is the long run number of employees expected in location C?
(Multiple Choice)
4.8/5  (26)
(26)
In the matrix of transition probabilities,Pij is the conditional probability of being in state i in the future,given the current state j.
(True/False)
4.8/5  (37)
(37)
When absorbing states exist,the fundamental matrix is used to compute equilibrium conditions.
(True/False)
4.9/5  (39)
(39)
Table 14-3
The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees.
A B C
P = ![Table 14-3 The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees. A B C P = π(0)= [1000,1000,1000] <sub> </sub><sub> </sub> -Using the data given in Table 14-3,how many employees do we expect in location B one year from now?](https://storage.examlex.com/TB2950/11eabb83_5a40_619b_b8db_d18cdc104bec_TB2950_11_TB2950_11_TB2950_11_TB2950_11_TB2950_11.jpg)
![Table 14-3 The following data consists of a matrix of transition probabilities (P)of three office locations (A,B,C)within a large company and how employees shift from one location to the other from year to year.The company CEO would like to understand the movement of employees over time and the long-run proportion of employees in each location.Assume that there is always a total of 3000 employees. A B C P = π(0)= [1000,1000,1000] <sub> </sub><sub> </sub> -Using the data given in Table 14-3,how many employees do we expect in location B one year from now?](https://storage.examlex.com/TB2950/11eabb83_5a40_88ac_b8db_cb9f435fda4b_TB2950_11_TB2950_11_TB2950_11_TB2950_11_TB2950_11.jpg) π(0)= [1000,1000,1000]
-Using the data given in Table 14-3,how many employees do we expect in location B one year from now?
π(0)= [1000,1000,1000]
-Using the data given in Table 14-3,how many employees do we expect in location B one year from now?
(Multiple Choice)
4.9/5  (38)
(38)
If in an absorbing state,the probability of being in an absorbing state in the future is
(Multiple Choice)
4.9/5  (35)
(35)
Describe the concept of "collectively exhaustive" in the context of Markov analysis.
(Essay)
4.8/5  (32)
(32)
Given the following matrix of transition probabilities,write three equations that,when solved,will give the equilibrium state values.
P = 
(Essay)
4.7/5  (32)
(32)
The weather is becoming important to you since you would like to go on a picnic today.If it was sunny yesterday,there is a 70% chance it will be sunny today.If it was raining yesterday,there is a 30% chance it will be sunny today.If the probability that it was raining yesterday is 0.25,what is the probability that it will rain today?
(Multiple Choice)
4.8/5  (40)
(40)
The weather is becoming important to you since you would like to go on a picnic today.If it was sunny yesterday,there is a 70% chance it will be sunny today.If it was raining yesterday,there is a 30% chance it will be sunny today.What is the probability it will be rainy today,if it was sunny yesterday?
(Multiple Choice)
4.9/5  (34)
(34)
Showing 21 - 40 of 86
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)