Exam 6: The Normal Distribution and Other Continuous Distributions

TABLE 6-3 Suppose the time interval between two consecutive defective light bulbs from a production line has a uniform distribution over an interval from 0 to 90 minutes. -Referring to Table 6-3,what is the probability that the time interval between two consecutive defective light bulbs will be between 10 and 35 minutes?

True or False: The probability that a standard normal variable,Z,is between 1.50 and 2.10 is the same as the probability Z is between -2.10 and -1.50.

TABLE 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month,plus a commission.His monthly commission is normally distributed with a mean of $10,000 and a standard deviation of $2,000.At night he works occasionally as a waiter,for which his monthly income is normally distributed with a mean of $1,000 and a standard deviation of $300.John's income levels from these two sources are independent of each other. -Referring to Table 6-2,for a given month,what is the probability that John's commission from the jewelry store is between $5,000 and $7,000?

TABLE 6-5 A company producing orange juice buys all of its oranges from a large orange orchard.The amount of juice that can be squeezed from each of these oranges is approximately normally distributed with a mean of 4.7 ounces and some unknown standard deviation.The company's production manager knows that the probability is 30.85% that a randomly selected orange will contain less than 4.5 ounces of juice.Also,the probability is 10.56% that a randomly selected orange will contain more than 5.2 ounces of juice.Answer the following questions without the help of a calculator,statistical software or statistical table. -Referring to Table 6-5,what is the probability that a randomly selected orange will contain between 4.5 and 5.2 ounces of juice?

TABLE 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month,plus a commission.His monthly commission is normally distributed with a mean of $10,000 and a standard deviation of $2,000.At night he works occasionally as a waiter,for which his monthly income is normally distributed with a mean of $1,000 and a standard deviation of $300.John's income levels from these two sources are independent of each other. -Referring to Table 6-2,John's income as a waiter will be between what two values symmetrically distributed around the population mean 90% of the time?

If we know that the length of time it takes a college student to find a parking spot in the library parking lot follows a normal distribution with a mean of 3.5 minutes and a standard deviation of 1 minute,75.8% of the college students will take more than how many minutes when trying to find a parking spot in the library parking lot?

The amount of juice that can be squeezed from a randomly selected orange out of a box of oranges with approximately the same size can most likely be modeled by which of the following distributions?

Let X represent the amount of time until the next student will arrive in the library parking lot at the university.If we know that the distribution of arrival time can be modeled using an exponential distribution with a mean of 4 minutes (i.e.the mean number of arrivals is per minute),find the probability that it will take more than 10 minutes for the next student to arrive at the library parking lot.

TABLE 6-6 According to Investment Digest,the arithmetic mean of the annual return for common stocks over an 85-year period was 9.5%,but the value of the variance was not mentioned.Also 25% of the annual returns were below 8%,while 65% of the annual returns were between 8% and 11.5%.The article claimed that the distribution of annual return for common stocks was bell-shaped and approximately symmetric.Assume that this distribution is normal with the mean given above.Answer the following questions without the help of a calculator,statistical software or statistical table. -Referring to Table 6-6,find the probability that the annual return of a random year will be more than 7.5%.

You were told that the amount of time lapsed between consecutive trades on the New York Stock Exchange followed a normal distribution with a mean of 15 seconds.You were also told that the probability that the time lapsed between two consecutive trades to fall between 16 to 17 seconds was 13%.The probability that the time lapsed between two consecutive trades would fall below 13 seconds was 7%.What is the probability that the time lapsed between two consecutive trades will be between 15 and 16 seconds?

The owner of a fish market determined that the average weight for a catfish is 3.2 pounds with a standard deviation of 0.8 pound.Assuming the weights of catfish are normally distributed,above what weight (in pounds)do 89.80% of the weights occur?

Given that X is a normally distributed variable with a mean of 50 and a standard deviation of 2,find the probability that X is between 47 and 54.

You were told that the amount of time lapsed between consecutive trades on the New York Stock Exchange followed a normal distribution with a mean of 15 seconds.You were also told that the probability that the time lapsed between two consecutive trades to fall between 16 to 17 seconds was 13%.The probability that the time lapsed between two consecutive trades would fall below 13 seconds was 7%.What is the probability that the time lapsed between two consecutive trades will be longer than 17 seconds?

TABLE 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month,plus a commission.His monthly commission is normally distributed with a mean of $10,000 and a standard deviation of $2,000.At night he works occasionally as a waiter,for which his monthly income is normally distributed with a mean of $1,000 and a standard deviation of $300.John's income levels from these two sources are independent of each other. -Referring to Table 6-2,the probability is 0.10 that John's commission from the jewelry store is more than how much in a given month?

The amount of time necessary for assembly line workers to complete a product is a normal variable with a mean of 15 minutes and a standard deviation of 2 minutes.The probability is ________ that a product is assembled in more than 19 minutes.

The amount of time necessary for assembly line workers to complete a product is a normal variable with a mean of 15 minutes and a standard deviation of 2 minutes.The probability is ________ that a product is assembled in less than 20 minutes.

TABLE 6-2 John has two jobs.For daytime work at a jewelry store he is paid $15,000 per month,plus a commission.His monthly commission is normally distributed with a mean of $10,000 and a standard deviation of $2,000.At night he works occasionally as a waiter,for which his monthly income is normally distributed with a mean of $1,000 and a standard deviation of $300.John's income levels from these two sources are independent of each other. -Referring to Table 6-2,for a given month,what is the probability that John's income as a waiter is more than $900?

A catalog company that receives the majority of its orders by telephone conducted a study to determine how long customers were willing to wait on hold before ordering a product.The length of waiting time was found to be a variable best approximated by an exponential distribution with a mean length of waiting time equal to 2.8 minutes (i.e.the mean number of calls answered in a minute is 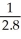).What is the probability that a randomly selected caller is placed on hold fewer than 7 minutes?

In its standardized form,the normal distribution

The owner of a fish market determined that the average weight for a catfish is 3.2 pounds with a standard deviation of 0.8 pound.Assuming the weights of catfish are normally distributed,the probability that a randomly selected catfish will weigh less than 2.2 pounds is ________.