Exam 15: Multiple Regression Model Building
Exam 1: Instruction and Data Collection47 Questions
Exam 2: Presenting Data in Tables and Charts277 Questions
Exam 3: Numerical Descriptive Measures139 Questions
Exam 4: Basic Probability137 Questions
Exam 5: Some Important Discrete Probability Distributions188 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions164 Questions
Exam 7: Sampling and Sampling Distributions187 Questions
Exam 8: Confidence Interval Estimation173 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests146 Questions
Exam 10: Two-Sample Tests190 Questions
Exam 11: Analysis of Variance127 Questions
Exam 12: Chi-Square Tests and Nonparametric Tests174 Questions
Exam 13: Simple Linear Regression198 Questions
Exam 14: Introduction to Multiple Regression215 Questions
Exam 15: Multiple Regression Model Building101 Questions
Exam 16: Time-Series Analysis and Index Numbers133 Questions
Exam 17: Statistical Applications in Quality Management132 Questions
Exam 18: Data Analysis Overview52 Questions
Select questions type
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
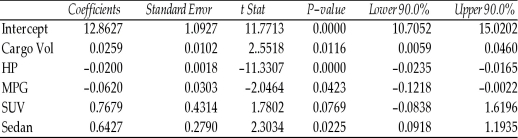
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

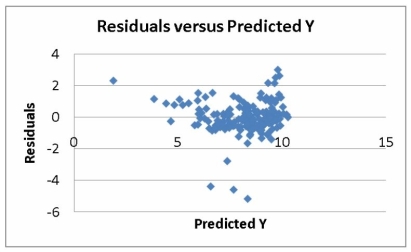
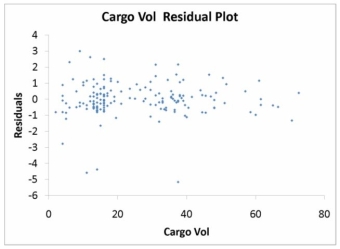
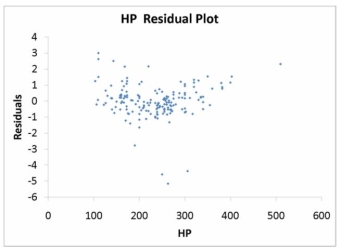
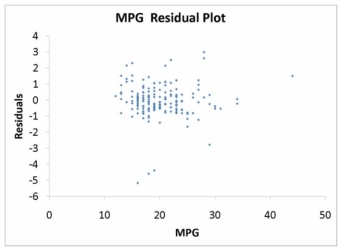
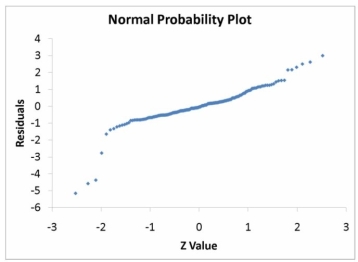
 The various residual plots are as shown below.
The various residual plots are as shown below.
 The coefficient of partial determination (
The coefficient of partial determination ( 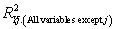 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 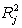 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, the 0 to 60 miles per hour acceleration time of a coupe is predicted to be 0.7679 seconds higher than that of a sedan.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, the 0 to 60 miles per hour acceleration time of a coupe is predicted to be 0.7679 seconds higher than that of a sedan.
(True/False)
4.9/5  (32)
(32)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered."
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA
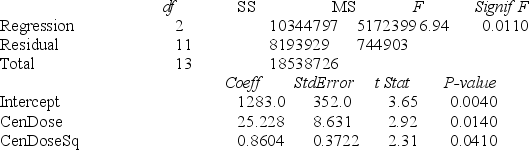 -Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.05, she would decide that there is a significant curvilinear relationship.
-Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.05, she would decide that there is a significant curvilinear relationship.
(True/False)
4.8/5  (28)
(28)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 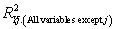 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 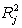 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, there is enough evidence to conclude that Cargo Vol makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, there is enough evidence to conclude that Cargo Vol makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance.
(True/False)
4.9/5  (35)
(35)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable, X1 = % Attendance, X2 = Salaries and X3 = Spending.
The coefficient of multiple determination (Rj 2) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743.
The output from the best-subset regressions is given below:
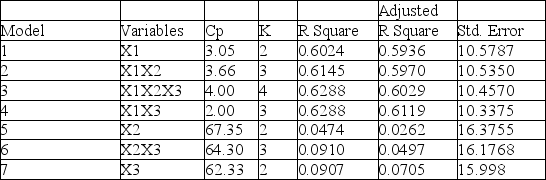 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
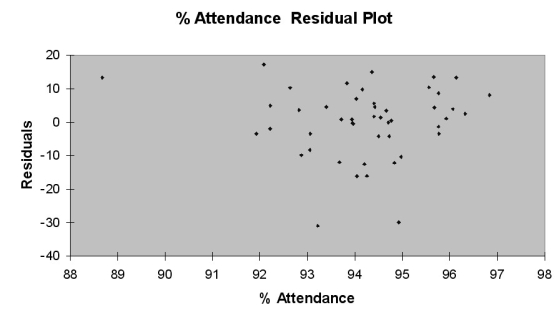 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
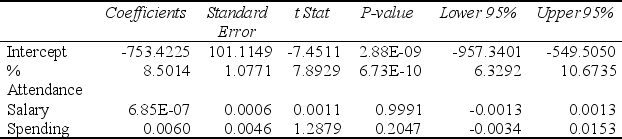 Model (II):
Model (II):
 Model (III):
Model (III):
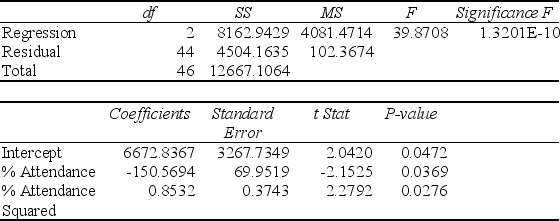 -Referring to Table 15-4, the null hypothesis should be rejected when testing whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance.
-Referring to Table 15-4, the null hypothesis should be rejected when testing whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance.
(True/False)
4.8/5  (42)
(42)
Collinearity will result in excessively low standard errors of the parameter estimates reported in the regression output.
(True/False)
4.9/5  (38)
(38)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 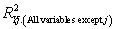 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 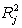 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, what is the value of the test statistic to determine whether MPG makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance?
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, what is the value of the test statistic to determine whether MPG makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance?
(Short Answer)
4.8/5  (34)
(34)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 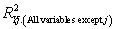 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 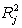 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by the five independent variables after taking into consideration the number of independent variables and the number of observations.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by the five independent variables after taking into consideration the number of independent variables and the number of observations.
(Short Answer)
4.8/5  (41)
(41)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 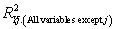 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 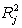 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, what is the correct interpretation for the estimated coefficient for SUV?
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, what is the correct interpretation for the estimated coefficient for SUV?
(Multiple Choice)
4.8/5  (44)
(44)
One of the consequences of collinearity in multiple regression is biased estimates on the slope coefficients.
(True/False)
4.7/5  (37)
(37)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable, X1 = % Attendance, X2 = Salaries and X3 = Spending.
The coefficient of multiple determination (Rj 2) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743.
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
 -Referring to Table 15-4, the "best" model using a 5% level of significance among those chosen by the Cp statistic is
-Referring to Table 15-4, the "best" model using a 5% level of significance among those chosen by the Cp statistic is
(Multiple Choice)
4.8/5  (34)
(34)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 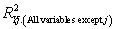 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 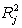 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, there is enough evidence to conclude that MPG makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, there is enough evidence to conclude that MPG makes a significant contribution to the regression model in the presence of the other independent variables at a 5% level of significance.
(True/False)
4.9/5  (35)
(35)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 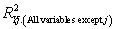 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 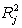 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by Cargo Vol while controlling for the other independent variables.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by Cargo Vol while controlling for the other independent variables.
(Short Answer)
4.9/5  (26)
(26)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable, X1 = % Attendance, X2 = Salaries and X3 = Spending.
The coefficient of multiple determination (Rj 2) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743.
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
 -Referring to Table 15-4, what is the value of the test statistic to determine whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance?
-Referring to Table 15-4, what is the value of the test statistic to determine whether the quadratic effect of daily average of the percentage of students attending class on percentage of students passing the proficiency test is significant at a 5% level of significance?
(Short Answer)
4.9/5  (44)
(44)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 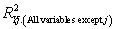 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 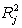 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, what is the correct interpretation for the estimated coefficient for Cargo Vol?
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, what is the correct interpretation for the estimated coefficient for Cargo Vol?
(Multiple Choice)
4.8/5  (28)
(28)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered."
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA
 -Referring to Table 15-3, suppose the chemist decides to use a t test to determine if there is a significant difference between a curvilinear model without a linear term and a curvilinear model that includes a linear term. The p-value of the test is ________.
-Referring to Table 15-3, suppose the chemist decides to use a t test to determine if there is a significant difference between a curvilinear model without a linear term and a curvilinear model that includes a linear term. The p-value of the test is ________.
(Short Answer)
4.9/5  (42)
(42)
TABLE 15-1
A certain type of rare gem serves as a status symbol for many of its owners. In theory, for low prices, the demand increases and it decreases as the price of the gem increases. However, experts hypothesize that when the gem is valued at very high prices, the demand increases with price due to the status owners believe they gain in obtaining the gem. Thus, the model proposed to best explain the demand for the gem by its price is the quadratic model:
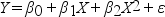 where Y = demand (in thousands) and X = retail price per carat.
This model was fit to data collected for a sample of 12 rare gems of this type. A portion of the computer analysis obtained from Microsoft Excel is shown below:
SUMMARY OUTPUT
Regression Statistics
where Y = demand (in thousands) and X = retail price per carat.
This model was fit to data collected for a sample of 12 rare gems of this type. A portion of the computer analysis obtained from Microsoft Excel is shown below:
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA

 -Referring to Table 15-1, what is the correct interpretation of the coefficient of multiple determination?
-Referring to Table 15-1, what is the correct interpretation of the coefficient of multiple determination?
(Multiple Choice)
4.8/5  (36)
(36)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 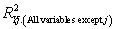 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 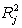 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, there is reason to suspect collinearity between some pairs of predictors based on the values of the variance inflationary factor.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, there is reason to suspect collinearity between some pairs of predictors based on the values of the variance inflationary factor.
(True/False)
4.8/5  (31)
(31)
In stepwise regression, an independent variable is not allowed to be removed from the model once it has entered into the model.
(True/False)
4.9/5  (31)
(31)
TABLE 15-1
A certain type of rare gem serves as a status symbol for many of its owners. In theory, for low prices, the demand increases and it decreases as the price of the gem increases. However, experts hypothesize that when the gem is valued at very high prices, the demand increases with price due to the status owners believe they gain in obtaining the gem. Thus, the model proposed to best explain the demand for the gem by its price is the quadratic model:
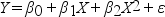 where Y = demand (in thousands) and X = retail price per carat.
This model was fit to data collected for a sample of 12 rare gems of this type. A portion of the computer analysis obtained from Microsoft Excel is shown below:
SUMMARY OUTPUT
Regression Statistics
where Y = demand (in thousands) and X = retail price per carat.
This model was fit to data collected for a sample of 12 rare gems of this type. A portion of the computer analysis obtained from Microsoft Excel is shown below:
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA

 -Referring to Table 15-1, a more parsimonious simple linear model is likely to be statistically superior to the fitted curvilinear for predicting sale price (Y).
-Referring to Table 15-1, a more parsimonious simple linear model is likely to be statistically superior to the fitted curvilinear for predicting sale price (Y).
(True/False)
4.9/5  (33)
(33)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 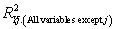 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 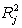 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, the error appears to be normally distributed.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, the error appears to be normally distributed.
(True/False)
4.7/5  (32)
(32)
Showing 81 - 100 of 101
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)