Exam 15: Multiple Regression Model Building
Exam 1: Instruction and Data Collection47 Questions
Exam 2: Presenting Data in Tables and Charts277 Questions
Exam 3: Numerical Descriptive Measures139 Questions
Exam 4: Basic Probability137 Questions
Exam 5: Some Important Discrete Probability Distributions188 Questions
Exam 6: The Normal Distribution and Other Continuous Distributions164 Questions
Exam 7: Sampling and Sampling Distributions187 Questions
Exam 8: Confidence Interval Estimation173 Questions
Exam 9: Fundamentals of Hypothesis Testing: One-Sample Tests146 Questions
Exam 10: Two-Sample Tests190 Questions
Exam 11: Analysis of Variance127 Questions
Exam 12: Chi-Square Tests and Nonparametric Tests174 Questions
Exam 13: Simple Linear Regression198 Questions
Exam 14: Introduction to Multiple Regression215 Questions
Exam 15: Multiple Regression Model Building101 Questions
Exam 16: Time-Series Analysis and Index Numbers133 Questions
Exam 17: Statistical Applications in Quality Management132 Questions
Exam 18: Data Analysis Overview52 Questions
Select questions type
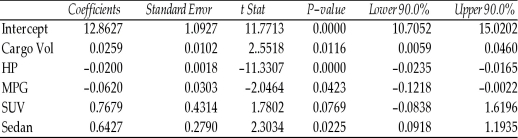
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

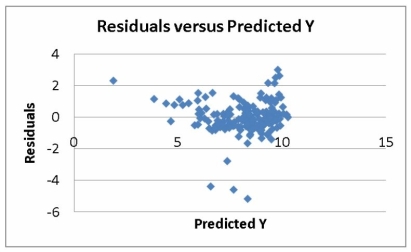
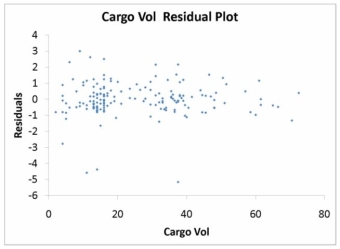
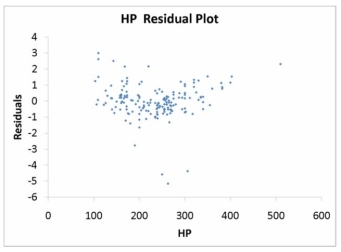
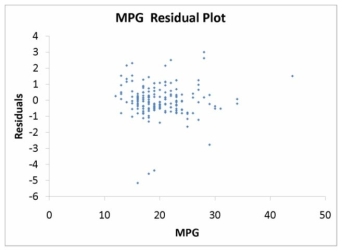
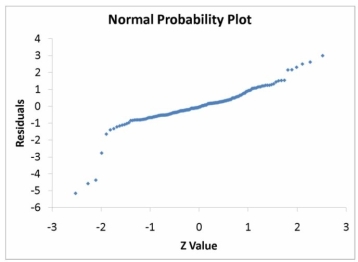
 The various residual plots are as shown below.
The various residual plots are as shown below.
 The coefficient of partial determination (
The coefficient of partial determination ( 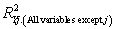 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 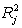 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by MPG while controlling for the other independent variables.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by MPG while controlling for the other independent variables.
(Short Answer)
4.9/5  (30)
(30)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 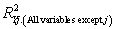 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 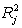 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by the five independent variables.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by the five independent variables.
(Short Answer)
4.8/5  (30)
(30)
TABLE 15-2
In Hawaii, condemnation proceedings are under way to enable private citizens to own the property that their homes are built on. Until recently, only estates were permitted to own land, and homeowners leased the land from the estate. In order to comply with the new law, a large Hawaiian estate wants to use regression analysis to estimate the fair market value of the land. The following model was fit to data collected for n = 20 properties, 10 of which are located near a cove.
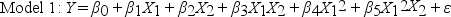
 Using the data collected for the 20 properties, the following partial output obtained from Microsoft Excel is shown:
SUMMARY OUTPUT
Regression Statistics
Using the data collected for the 20 properties, the following partial output obtained from Microsoft Excel is shown:
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA

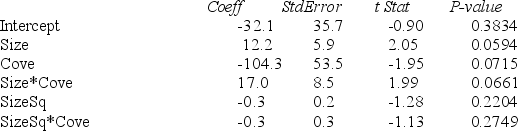 -Referring to Table 15-2, given a quadratic relationship between sale price (Y) and property size (X1), what null hypothesis would you test to determine whether the curves differ from cove and non-cove properties?
-Referring to Table 15-2, given a quadratic relationship between sale price (Y) and property size (X1), what null hypothesis would you test to determine whether the curves differ from cove and non-cove properties?
(Multiple Choice)
4.9/5  (36)
(36)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 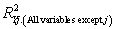 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 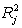 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, the 0 to 60 miles per hour acceleration time of a sedan is predicted to be 0.6427 seconds higher than that of an SUV.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, the 0 to 60 miles per hour acceleration time of a sedan is predicted to be 0.6427 seconds higher than that of an SUV.
(True/False)
4.8/5  (34)
(34)
So that we can fit curves as well as lines by regression, we often use mathematical manipulations for converting one variable into a different form. These manipulations are called dummy variables.
(True/False)
4.8/5  (30)
(30)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered."
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA
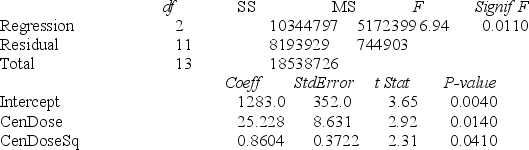 -Referring to Table 15-3, suppose the chemist decides to use a t test to determine if there is a significant difference between a curvilinear model without a linear term and a curvilinear model that includes a linear term. The value of the test statistic is ________.
-Referring to Table 15-3, suppose the chemist decides to use a t test to determine if there is a significant difference between a curvilinear model without a linear term and a curvilinear model that includes a linear term. The value of the test statistic is ________.
(Short Answer)
4.9/5  (26)
(26)
As a project for his business statistics class, a student examined the factors that determined parking meter rates throughout the campus area. Data were collected for the price per hour of parking, blocks to the quadrangle, and one of the three jurisdictions: on campus, in downtown and off campus, or outside of downtown and off campus. The population regression model hypothesized is Yi = α + β0 + β1X1i + β2X2i + β3X3i + ε
Where
Y is the meter price
X1 is the number of blocks to the quad
X2 is a dummy variable that takes the value 1 if the meter is located in downtown and off campus and the value 0 otherwise
X3 is a dummy variable that takes the value 1 if the meter is located outside of downtown and off campus, and the value 0 otherwise
Suppose that whether the meter is located on campus is an important explanatory factor. Why should the variable that depicts this attribute not be included in the model?
(Multiple Choice)
4.8/5  (37)
(37)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered."
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA
 -Referring to Table 15-3, suppose the chemist decides to use a t test to determine if there is a significant difference between a curvilinear model without a linear term and a curvilinear model that includes a linear term. Using a level of significance of 0.05, she would decide that the curvilinear model should include a linear term.
-Referring to Table 15-3, suppose the chemist decides to use a t test to determine if there is a significant difference between a curvilinear model without a linear term and a curvilinear model that includes a linear term. Using a level of significance of 0.05, she would decide that the curvilinear model should include a linear term.
(True/False)
5.0/5  (31)
(31)
The parameter estimates are biased when collinearity is present in a multiple regression equation.
(True/False)
4.7/5  (34)
(34)
TABLE 15-3
A chemist employed by a pharmaceutical firm has developed a muscle relaxant. She took a sample of 14 people suffering from extreme muscle constriction. She gave each a vial containing a dose (X) of the drug and recorded the time to relief (Y) measured in seconds for each. She fit a "centered" curvilinear model to this data. The results obtained by Microsoft Excel follow, where the dose (X) given has been "centered."
SUMMARY OUTPUT
Regression Statistics
 ANOVA
ANOVA
 -Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.01 she would decide that there is a significant curvilinear relationship.
-Referring to Table 15-3, suppose the chemist decides to use an F test to determine if there is a significant curvilinear relationship between time and dose. If she chooses to use a level of significance of 0.01 she would decide that there is a significant curvilinear relationship.
(True/False)
4.8/5  (34)
(34)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable, X1 = % Attendance, X2 = Salaries and X3 = Spending.
The coefficient of multiple determination (Rj 2) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743.
The output from the best-subset regressions is given below:
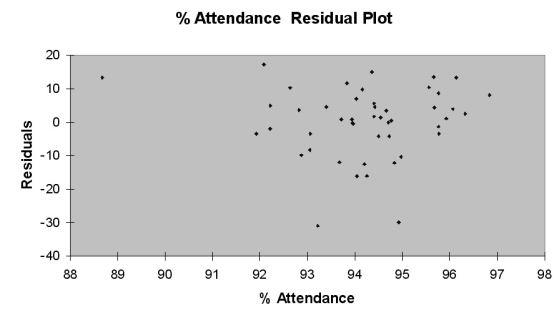
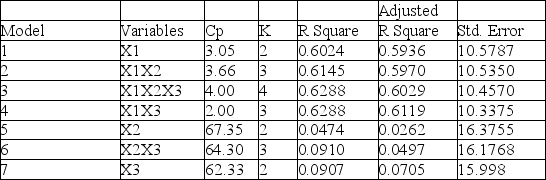 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
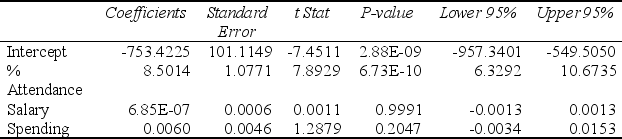
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
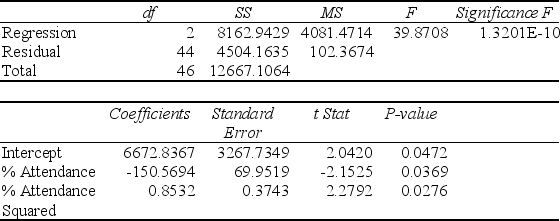 -Referring to Table 15-4, the "best" model chosen using the adjusted R-square statistic is
-Referring to Table 15-4, the "best" model chosen using the adjusted R-square statistic is
(Multiple Choice)
4.8/5  (35)
(35)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable, X1 = % Attendance, X2 = Salaries and X3 = Spending.
The coefficient of multiple determination (Rj 2) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743.
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
 -Referring to Table 15-4, there is reason to suspect collinearity between some pairs of predictors.
-Referring to Table 15-4, there is reason to suspect collinearity between some pairs of predictors.
(True/False)
4.8/5  (31)
(31)
A regression diagnostic tool used to study the possible effects of collinearity is ________.
(Short Answer)
4.8/5  (32)
(32)
An independent variable Xj is considered highly correlated with the other independent variables if
(Multiple Choice)
4.9/5  (28)
(28)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 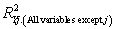 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 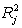 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, which of the following assumptions is most likely violated based on the residual plot of the residuals versus predicted Y?
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, which of the following assumptions is most likely violated based on the residual plot of the residuals versus predicted Y?
(Multiple Choice)
4.8/5  (36)
(36)
TABLE 15-4
The superintendent of a school district wanted to predict the percentage of students passing a sixth-grade proficiency test. She obtained the data on percentage of students passing the proficiency test (% Passing), daily average of the percentage of students attending class (% Attendance), average teacher salary in dollars (Salaries), and instructional spending per pupil in dollars (Spending) of 47 schools in the state.
Let Y = % Passing as the dependent variable, X1 = % Attendance, X2 = Salaries and X3 = Spending.
The coefficient of multiple determination (Rj 2) of each of the 3 predictors with all the other remaining predictors are, respectively, 0.0338, 0.4669, and 0.4743.
The output from the best-subset regressions is given below:
 Following is the residual plot for % Attendance:
Following is the residual plot for % Attendance:
 Following is the output of several multiple regression models:
Model (I):
Following is the output of several multiple regression models:
Model (I):
 Model (II):
Model (II):
 Model (III):
Model (III):
 -Referring to Table 15-4, what are, respectively, the values of the variance inflationary factor of the 3 predictors?
-Referring to Table 15-4, what are, respectively, the values of the variance inflationary factor of the 3 predictors?
(Short Answer)
4.8/5  (33)
(33)
TABLE 15-5
What are the factors that determine the acceleration time (in sec.) from 0 to 60 miles per hour of a car? Data on the following variables for 171 different vehicle models were collected:
Accel Time: Acceleration time in sec.
Cargo Vol: Cargo volume in cu. ft.
HP: Horsepower
MPG: Miles per gallon
SUV: 1 if the vehicle model is an SUV with Coupe as the base when SUV and Sedan are both 0
Sedan: 1 if the vehicle model is a sedan with Coupe as the base when SUV and Sedan are both 0
The regression results using acceleration time as the dependent variable and the remaining variables as the independent variables are presented below.
 ANOVA
ANOVA

 The various residual plots are as shown below.
The various residual plots are as shown below.




 The coefficient of partial determination (
The coefficient of partial determination ( 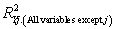 ) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables (
) of each of the 5 predictors are, respectively, 0.0380, 0.4376, 0.0248, 0.0188, and 0.0312.
The coefficient of multiple determination for the regression model using each of the 5 variables as the dependent variable and all other X variables as independent variables ( 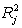 ) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by HP while controlling for the other independent variables.
) are, respectively, 0.7461, 0.5676, 0.6764, 0.8582, 0.6632.
-Referring to Table 15-5, ________ of the variation in Accel Time can be explained by HP while controlling for the other independent variables.
(Short Answer)
4.9/5  (41)
(41)
Showing 41 - 60 of 101
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)