Exam 13: Partial Derivatives
Exam 1: Limits and Continuity186 Questions
Exam 2: The Derivative198 Questions
Exam 3: Topics in Deifferentiation171 Questions
Exam 4: The Derivative in Graphing and Applications656 Questions
Exam 5: Integration323 Questions
Exam 6: Applications of the Definite Integral in Geometry, Science and Engineering314 Questions
Exam 7: Principle of Integral Evaluation269 Questions
Exam 8: Mathematical Modeling With Differential Equations77 Questions
Exam 9: Infinte Series288 Questions
Exam 10: Parametric and Polar Curves; Conic Sections199 Questions
Exam 11: Three-Dimensional Space; Vectors173 Questions
Exam 12: Vector-Valued Functions147 Questions
Exam 13: Partial Derivatives194 Questions
Exam 14: Multiple Integrals117 Questions
Exam 15: Topics in Vector Calculus149 Questions
Select questions type
The legs of a right triangle are measured to be 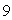 and
and 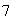 inches with a maximum error of
inches with a maximum error of 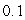 inches in each measurement. Use differentials to estimate the maximum possible error in the calculated value of the area.
inches in each measurement. Use differentials to estimate the maximum possible error in the calculated value of the area.
(Multiple Choice)
4.8/5  (46)
(46)
A rectangular box, open at the top, is to contain 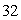 cubic inches. Find the dimensions of the box for which the surface area is a minimum.
cubic inches. Find the dimensions of the box for which the surface area is a minimum.
(Multiple Choice)
4.8/5  (31)
(31)
Use the chain rule to find 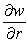 and
and 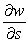 if w = -16 + ln (x2 + y2 + 2z), x = r + s, y = r - s, z = 2rs.
if w = -16 + ln (x2 + y2 + 2z), x = r + s, y = r - s, z = 2rs.
(Essay)
4.8/5  (33)
(33)
The lengths and widths of a rectangle are measured with errors of at most 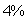 . Use differentials to estimate the maximum percentage error in the calculated area.
. Use differentials to estimate the maximum percentage error in the calculated area.
(Essay)
4.9/5  (38)
(38)
Determine whether the function 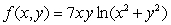 has a removable discontinuity at the origin.
has a removable discontinuity at the origin.
(Short Answer)
5.0/5  (39)
(39)
Use Lagrange multipliers to find all the locations of the extreme values of 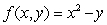 subject to
subject to 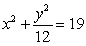 .
.
(Multiple Choice)
4.8/5  (34)
(34)
Determine whether the function 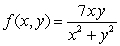 has a removable discontinuity at the origin.
has a removable discontinuity at the origin.
(Short Answer)
4.8/5  (36)
(36)
An open rectangular box is to contain 256 cubic inches. Use the Lagrange multiplier method to find the dimensions of the box which uses the least amount of material.
(Short Answer)
4.8/5  (29)
(29)
A particle is located at the point (5, 5) on a metal surface whose temperature at a point (x, y) is T(x, y) = 25 - 3x2 - 2y2. Find the equation for the trajectory of a particle moving continuously in the direction of maximum temperature increase. y =
(Multiple Choice)
4.7/5  (45)
(45)
Showing 101 - 120 of 194
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)